
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science.

In optics, the refractive index of an optical medium is a dimensionless number that gives the indication of the light bending ability of that medium.

In quantum mechanics, the uncertainty principle is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physical quantities of a particle, such as position, x, and momentum, p, can be predicted from initial conditions.

Bremsstrahlung, from bremsen "to brake" and Strahlung "radiation"; i.e., "braking radiation" or "deceleration radiation", is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into radiation, thus satisfying the law of conservation of energy. The term is also used to refer to the process of producing the radiation. Bremsstrahlung has a continuous spectrum, which becomes more intense and whose peak intensity shifts toward higher frequencies as the change of the energy of the decelerated particles increases.

The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the subject. The equation is named after Erwin Schrödinger, who postulated the equation in 1925, and published it in 1926, forming the basis for the work that resulted in his Nobel Prize in Physics in 1933.
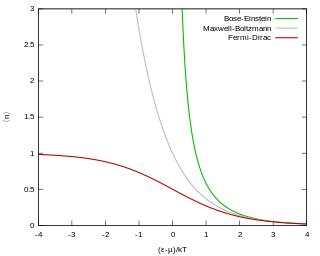
Fermi–Dirac statistics is a type of quantum statistics that applies to the physics of a system consisting of many non-interacting, identical particles that obey the Pauli exclusion principle. A result is the Fermi–Dirac distribution of particles over energy states. It is named after Enrico Fermi and Paul Dirac, each of whom derived the distribution independently in 1926. Fermi–Dirac statistics is a part of the field of statistical mechanics and uses the principles of quantum mechanics.

In physics, Planck's law describes the spectral density of electromagnetic radiation emitted by a black body in thermal equilibrium at a given temperature T, when there is no net flow of matter or energy between the body and its environment.
In spectroscopy, the Rydberg constant, symbol for heavy atoms or for hydrogen, named after the Swedish physicist Johannes Rydberg, is a physical constant relating to the electromagnetic spectra of an atom. The constant first arose as an empirical fitting parameter in the Rydberg formula for the hydrogen spectral series, but Niels Bohr later showed that its value could be calculated from more fundamental constants via his Bohr model.

The path integral formulation is a description in quantum mechanics that generalizes the action principle of classical mechanics. It replaces the classical notion of a single, unique classical trajectory for a system with a sum, or functional integral, over an infinity of quantum-mechanically possible trajectories to compute a quantum amplitude.

In physics, a wave packet is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere. Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant or it may change (dispersion) while propagating.

In atomic physics, the fine structure describes the splitting of the spectral lines of atoms due to electron spin and relativistic corrections to the non-relativistic Schrödinger equation. It was first measured precisely for the hydrogen atom by Albert A. Michelson and Edward W. Morley in 1887, laying the basis for the theoretical treatment by Arnold Sommerfeld, introducing the fine-structure constant.

In quantum mechanics and quantum field theory, the propagator is a function that specifies the probability amplitude for a particle to travel from one place to another in a given period of time, or to travel with a certain energy and momentum. In Feynman diagrams, which serve to calculate the rate of collisions in quantum field theory, virtual particles contribute their propagator to the rate of the scattering event described by the respective diagram. These may also be viewed as the inverse of the wave operator appropriate to the particle, and are, therefore, often called (causal) Green's functions.
In quantum mechanics, the canonical commutation relation is the fundamental relation between canonical conjugate quantities. For example,
The Compton wavelength is a quantum mechanical property of a particle. The Compton wavelength of a particle is equal to the wavelength of a photon whose energy is the same as the rest energy of that particle. It was introduced by Arthur Compton in 1923 in his explanation of the scattering of photons by electrons.
Quantum noise is noise arising from the indeterminate state of matter in accordance with fundamental principles of quantum mechanics, specifically the uncertainty principle and via zero-point energy fluctuations. Quantum noise is due to the apparently discrete nature of the small quantum constituents such as electrons, as well as the discrete nature of quantum effects, such as photocurrents.
In quantum mechanics the delta potential is a potential well mathematically described by the Dirac delta function - a generalized function. Qualitatively, it corresponds to a potential which is zero everywhere, except at a single point, where it takes an infinite value. This can be used to simulate situations where a particle is free to move in two regions of space with a barrier between the two regions. For example, an electron can move almost freely in a conducting material, but if two conducting surfaces are put close together, the interface between them acts as a barrier for the electron that can be approximated by a delta potential.
Popper's experiment is an experiment proposed by the philosopher Karl Popper to put to the test different interpretations of quantum mechanics (QM). In fact, as early as 1934, Popper started criticising the increasingly more accepted Copenhagen interpretation, a popular subjectivist interpretation of quantum mechanics. Therefore, in his most famous book Logik der Forschung he proposed a first experiment alleged to empirically discriminate between the Copenhagen Interpretation and a realist interpretation, which he advocated. Einstein, however, wrote a letter to Popper about the experiment in which he raised some crucial objections and Popper himself declared that this first attempt was "a gross mistake for which I have been deeply sorry and ashamed of ever since".
The Planck constant, or Planck's constant, is a fundamental physical constant of foundational importance in quantum mechanics. The constant gives the relationship between the energy of a photon and its frequency, and by the mass-energy equivalence, the relationship between mass and frequency. Specifically, a photon's energy is equal to its frequency multiplied by the Planck constant. The constant is generally denoted by . The reduced Planck constant, or Dirac constant, equal to the constant divided by , is denoted by .

In quantum field theory, and in the significant subfields of quantum electrodynamics (QED) and quantum chromodynamics (QCD), the two-body Dirac equations (TBDE) of constraint dynamics provide a three-dimensional yet manifestly covariant reformulation of the Bethe–Salpeter equation for two spin-1/2 particles. Such a reformulation is necessary since without it, as shown by Nakanishi, the Bethe–Salpeter equation possesses negative-norm solutions arising from the presence of an essentially relativistic degree of freedom, the relative time. These "ghost" states have spoiled the naive interpretation of the Bethe–Salpeter equation as a quantum mechanical wave equation. The two-body Dirac equations of constraint dynamics rectify this flaw. The forms of these equations can not only be derived from quantum field theory they can also be derived purely in the context of Dirac's constraint dynamics and relativistic mechanics and quantum mechanics. Their structures, unlike the more familiar two-body Dirac equation of Breit, which is a single equation, are that of two simultaneous quantum relativistic wave equations. A single two-body Dirac equation similar to the Breit equation can be derived from the TBDE. Unlike the Breit equation, it is manifestly covariant and free from the types of singularities that prevent a strictly nonperturbative treatment of the Breit equation.
In quantum mechanics, the variational method is one way of finding approximations to the lowest energy eigenstate or ground state, and some excited states. This allows calculating approximate wavefunctions such as molecular orbitals. The basis for this method is the variational principle.





















