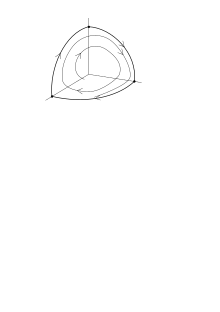
Robust heteroclinic cycles
A robust heteroclinic cycle is one which persists under small changes in the underlying dynamical system. Robust cycles often arise in the presence of symmetry or other constraints which force the existence of invariant hyperplanes. A prototypical example of a robust heteroclinic cycle is the Guckenheimer–Holmes cycle. This cycle has also been studied in the context of rotating convection, and as three competing species in population dynamics.