
Area is the quantity that expresses the extent of a two-dimensional region, shape, or planar lamina, in the plane. Surface area is its analog on the two-dimensional surface of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve or the volume of a solid.
In vector calculus and differential geometry, the generalized Stokes theorem, also called the Stokes–Cartan theorem, is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. It is a generalization of Isaac Newton's fundamental theorem of calculus that relates two-dimensional line integrals to three-dimensional surface integrals.

In mathematics, curvature is any of several strongly related concepts in geometry. Intuitively, the curvature is the amount by which a curve deviates from being a straight line, or a surface deviates from being a plane.
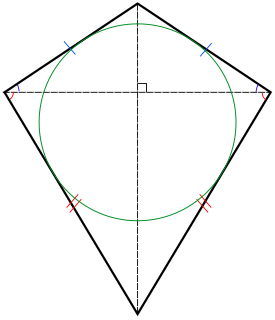
In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites, which often have this shape and which are in turn named for a bird. Kites are also known as deltoids, but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object.

The Gauss–Bonnet theorem, or Gauss–Bonnet formula, is a relationship between surfaces in differential geometry. It connects the curvature of a surface to its Euler characteristic.

In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.

In topology, a Jordan curve, sometimes called a plane simple closed curve, is a non-self-intersecting continuous loop in the plane. The Jordan curve theorem asserts that every Jordan curve divides the plane into an "interior" region bounded by the curve and an "exterior" region containing all of the nearby and far away exterior points, so that every continuous path connecting a point of one region to a point of the other intersects with that loop somewhere. While the statement of this theorem seems to be intuitively obvious, it takes some ingenuity to prove it by elementary means. "Although the JCT is one of the best known topological theorems, there are many, even among professional mathematicians, who have never read a proof of it.". More transparent proofs rely on the mathematical machinery of algebraic topology, and these lead to generalizations to higher-dimensional spaces.

A chord of a circle is a straight line segment whose endpoints both lie on a circular arc. The infinite line extension of a chord is a secant line, or just secant. More generally, a chord is a line segment joining two points on any curve, for instance, an ellipse. A chord that passes through a circle's center point is the circle's diameter. The word chord is from the Latin chorda meaning bowstring.
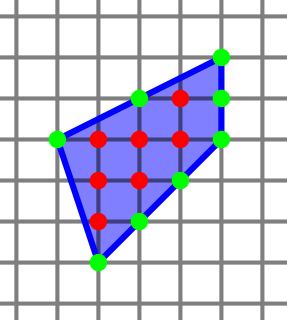
In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick in 1899, and popularized in English by Hugo Steinhaus in the 1950 edition of his book Mathematical Snapshots. It has multiple proofs, and can be generalized to formulas for certain kinds of non-simple polygons.

In geometry, a curve of constant width is a simple closed curve in the plane whose width is the same in all directions. The shape bounded by a curve of constant width is a body of constant width or an orbiform, the name given to these shapes by Leonhard Euler. Standard examples are the circle and the Reuleaux triangle. These curves can also be constructed using circular arcs centered at crossings of an arrangement of lines, as the involutes of certain curves, or by intersecting circles centered on a partial curve.

The classical four-vertex theorem of geometry states that the curvature function of a simple, closed, smooth plane curve has at least four local extrema. The name of the theorem derives from the convention of calling an extreme point of the curvature function a vertex. This theorem has many generalizations, including a version for space curves where a vertex is defined as a point of vanishing torsion.
The gradient theorem, also known as the fundamental theorem of calculus for line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve. The theorem is a generalization of the fundamental theorem of calculus to any curve in a plane or space rather than just the real line.

Viviani's theorem, named after Vincenzo Viviani, states that the sum of the distances from any interior point to the sides of an equilateral triangle equals the length of the triangle's altitude. It is a theorem commonly employed in various math competitions, secondary school mathematics examinations, and has wide applicability to many problems in the real world.
In mathematics, geometric measure theory (GMT) is the study of geometric properties of sets through measure theory. It allows mathematicians to extend tools from differential geometry to a much larger class of surfaces that are not necessarily smooth.

The Quadrature of the Parabola is a treatise on geometry, written by Archimedes in the 3rd century BC. Written as a letter to his friend Dositheus, the work presents 24 propositions regarding parabolas, culminating in a proof that the area of a parabolic segment is 4/3 that of a certain inscribed triangle.

In mathematics, the Pythagorean theorem, or Pythagoras's theorem, is a fundamental relation in Euclidean geometry among the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b and c, often called the Pythagorean equation:
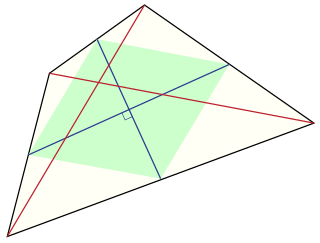
In Euclidean geometry, an equidiagonal quadrilateral is a convex quadrilateral whose two diagonals have equal length. Equidiagonal quadrilaterals were important in ancient Indian mathematics, where quadrilaterals were classified first according to whether they were equidiagonal and then into more specialized types.
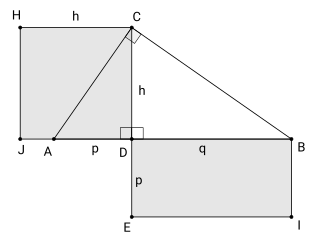
The right triangle altitude theorem or geometric mean theorem is a result in elementary geometry that describes a relation between the lengths of the altitude on the hypotenuse in a right triangle and the two line segments it creates on the hypotenuse. It states that the geometric mean of the two segments equals the altitude.
Rev. Hamnet Holditch, also spelled Hamnett Holditch, was an English mathematician who was president of Gonville and Caius College, Cambridge.
















