
In continuum mechanics, stress is a physical quantity that expresses the internal forces that neighbouring particles of a continuous material exert on each other, while strain is the measure of the deformation of the material. For example, when a solid vertical bar is supporting an overhead weight, each particle in the bar pushes on the particles immediately below it. When a liquid is in a closed container under pressure, each particle gets pushed against by all the surrounding particles. The container walls and the pressure-inducing surface push against them in (Newtonian) reaction. These macroscopic forces are actually the net result of a very large number of intermolecular forces and collisions between the particles in those molecules. Stress is frequently represented by a lowercase Greek letter sigma (σ).
A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.

In materials science, creep is the tendency of a solid material to move slowly or deform permanently under the influence of persistent mechanical stresses. It can occur as a result of long-term exposure to high levels of stress that are still below the yield strength of the material. Creep is more severe in materials that are subjected to heat for long periods and generally increases as they near their melting point.
Mohr–Coulomb theory is a mathematical model describing the response of brittle materials such as concrete, or rubble piles, to shear stress as well as normal stress. Most of the classical engineering materials somehow follow this rule in at least a portion of their shear failure envelope. Generally the theory applies to materials for which the compressive strength far exceeds the tensile strength.
The maximum distortion criterion considers that yielding of a ductile material begins when the second invariant of deviatoric stress reaches a critical value. It is part of plasticity theory that applies best to ductile materials, such as some metals. Prior to yield, material response can be assumed to be of a nonlinear elastic, viscoelastic, or linear elastic behavior.
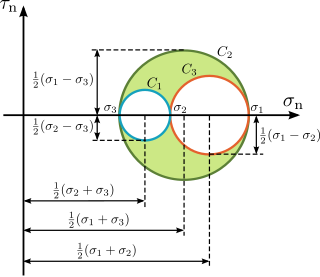
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor.

Work hardening, also known as strain hardening, is the strengthening of a metal or polymer by plastic deformation. Work hardening may be desirable, undesirable, or inconsequential, depending on the context.

In engineering, shear strength is the strength of a material or component against the type of yield or structural failure when the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is parallel to the direction of the force. When a paper is cut with scissors, the paper fails in shear.

In materials science and engineering, the yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning of plastic behavior. Below the yield point, a material will deform elastically and will return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible and is known as plastic deformation.

Critical resolved shear stress (CRSS) is the component of shear stress, resolved in the direction of slip, necessary to initiate slip in a grain. Resolved shear stress (RSS) is the shear component of an applied tensile or compressive stress resolved along a slip plane that is other than perpendicular or parallel to the stress axis. The RSS is related to the applied stress by a geometrical factor, m, typically the Schmid factor:
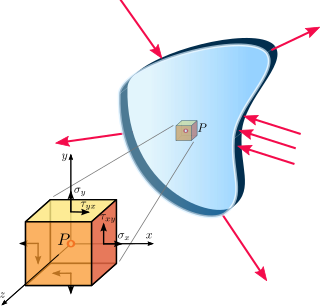
In continuum mechanics, a material is said to be under plane stress if the stress vector is zero across a particular plane. When that situation occurs over an entire element of a structure, as is often the case for thin plates, the stress analysis is considerably simplified, as the stress state can be represented by a tensor of dimension 2. A related notion, plane strain, is often applicable to very thick members.
The standard linear solid (SLS), also known as the Zener model, is a method of modeling the behavior of a viscoelastic material using a linear combination of springs and dashpots to represent elastic and viscous components, respectively. Often, the simpler Maxwell model and the Kelvin–Voigt model are used. These models often prove insufficient, however; the Maxwell model does not describe creep or recovery, and the Kelvin–Voigt model does not describe stress relaxation. SLS is the simplest model that predicts both phenomena.
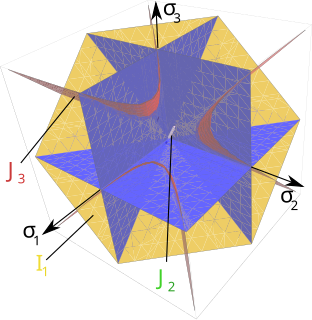
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the material is said to have become plastic. Further deformation of the material causes the stress state to remain on the yield surface, even though the shape and size of the surface may change as the plastic deformation evolves. This is because stress states that lie outside the yield surface are non-permissible in rate-independent plasticity, though not in some models of viscoplasticity.
Methods have been devised to modify the yield strength, ductility, and toughness of both crystalline and amorphous materials. These strengthening mechanisms give engineers the ability to tailor the mechanical properties of materials to suit a variety of different applications. For example, the favorable properties of steel result from interstitial incorporation of carbon into the iron lattice. Brass, a binary alloy of copper and zinc, has superior mechanical properties compared to its constituent metals due to solution strengthening. Work hardening has also been used for centuries by blacksmiths to introduce dislocations into materials, increasing their yield strengths.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
The Hill yield criterion developed by Rodney Hill, is one of several yield criteria for describing anisotropic plastic deformations. The earliest version was a straightforward extension of the von Mises yield criterion and had a quadratic form. This model was later generalized by allowing for an exponent m. Variations of these criteria are in wide use for metals, polymers, and certain composites.

Viscoplasticity is a theory in continuum mechanics that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation of the material depends on the rate at which loads are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep flow as a function of time under the influence of the applied load.

A fiber-reinforced composite (FRC) is a composite building material that consists of three components:
- the fibers as the discontinuous or dispersed phase,
- the matrix as the continuous phase, and
- the fine interphase region, also known as the interface.
The Hoek–Brown failure criterion is an empirical stress surface that is used in rock mechanics to predict the failure of rock. The original version of the Hoek–Brown criterion was developed by Evert Hoek and E. T. Brown in 1980 for the design of underground excavations. In 1988, the criterion was extended for applicability to slope stability and surface excavation problems. An update of the criterion was presented in 2002 that included improvements in the correlation between the model parameters and the geological strength index (GSI).
The unified strength theory (UST). proposed by Yu Mao-Hong is a series of yield criteria and failure criteria. It is a generalized classical strength theory which can be used to describe the yielding or failure of material begins when the combination of principal stresses reaches a critical value.














