In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children, but must be connected to exactly one parent, except for the root node, which has no parent. These constraints mean there are no cycles or "loops", and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes in a single straight line.

A tree structure, tree diagram, or tree model is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, although the chart is generally upside down compared to a biological tree, with the "stem" at the top and the "leaves" at the bottom.

In computer science, binary space partitioning (BSP) is a method for space partitioning which recursively subdivides a Euclidean space into two convex sets by using hyperplanes as partitions. This process of subdividing gives rise to a representation of objects within the space in the form of a tree data structure known as a BSP tree.

A scene graph is a general data structure commonly used by vector-based graphics editing applications and modern computer games, which arranges the logical and often spatial representation of a graphical scene. It is a collection of nodes in a graph or tree structure. A tree node may have many children but only a single parent, with the effect of a parent applied to all its child nodes; an operation performed on a group automatically propagates its effect to all of its members. In many programs, associating a geometrical transformation matrix at each group level and concatenating such matrices together is an efficient and natural way to process such operations. A common feature, for instance, is the ability to group related shapes and objects into a compound object that can then be manipulated as easily as a single object.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In information visualization and computing, treemapping is a method for displaying hierarchical data using nested figures, usually rectangles.

Daina Taimiņa is a Latvian mathematician, retired adjunct associate professor of mathematics at Cornell University, known for developing a way of modeling hyperbolic geometry with crocheted objects.

In geometric graph theory, a unit disk graph is the intersection graph of a family of unit disks in the Euclidean plane. That is, it is a graph with one vertex for each disk in the family, and with an edge between two vertices whenever the corresponding vertices lie within a unit distance of each other.

In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors. It describes a kaleidoscopic construction: each graph "node" represents a mirror and the label attached to a branch encodes the dihedral angle order between two mirrors, that is, the amount by which the angle between the reflective planes can be multiplied to get 180 degrees. An unlabeled branch implicitly represents order-3, and each pair of nodes that is not connected by a branch at all represents a pair of mirrors at order-2.
Visualization Library (VL) is an open source C++ middleware for 2D/3D graphics applications based on OpenGL 4, designed to develop portable applications for the Microsoft Windows, Linux and Mac OS X operating systems.
In graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices. Specifically, the removal of vertices from an n-vertex graph can partition the graph into disjoint subgraphs each of which has at most vertices.
In computational geometry, the fixed-radius near neighbor problem is a variant of the nearest neighbor search problem. In the fixed-radius near neighbor problem, one is given as input a set of points in d-dimensional Euclidean space and a fixed distance Δ. One must design a data structure that, given a query point q, efficiently reports the points of the data structure that are within distance Δ of q. The problem has long been studied; Bentley (1975) cites a 1966 paper by Levinthal that uses this technique as part of a system for visualizing molecular structures, and it has many other applications.

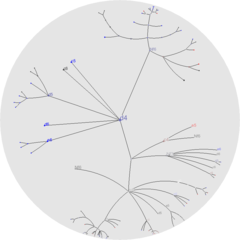
A radial tree, or radial map, is a method of displaying a tree structure in a way that expands outwards, radially. It is one of many ways to visually display a tree, with examples extending back to the early 20th century. In use, it is a type of information graphic.
SpicyNodes was a system for displaying hierarchical data, in which a focus node displays detailed information, and the surrounding nodes represent related information, with a layout based on radial maps. It has web (Flash) and mobile (iOS) implementations. It has ended operation as of 1 January 2018
In distributed computing and geometric graph theory, greedy embedding is a process of assigning coordinates to the nodes of a telecommunications network in order to allow greedy geographic routing to be used to route messages within the network. Although greedy embedding has been proposed for use in wireless sensor networks, in which the nodes already have positions in physical space, these existing positions may differ from the positions given to them by greedy embedding, which may in some cases be points in a virtual space of a higher dimension, or in a non-Euclidean geometry. In this sense, greedy embedding may be viewed as a form of graph drawing, in which an abstract graph is embedded into a geometric space.
In graph drawing, the area used by a drawing is a commonly used way of measuring its quality.

A hyperbolic geometric graph (HGG) or hyperbolic geometric network (HGN) is a special type of spatial network where (1) latent coordinates of nodes are sprinkled according to a probability density function into a hyperbolic space of constant negative curvature and (2) an edge between two nodes is present if they are close according to a function of the metric (typically either a Heaviside step function resulting in deterministic connections between vertices closer than a certain threshold distance, or a decaying function of hyperbolic distance yielding the connection probability). A HGG generalizes a random geometric graph (RGG) whose embedding space is Euclidean.
In discrete mathematics and theoretical computer science, the rotation distance between two binary trees with the same number of nodes is the minimum number of tree rotations needed to reconfigure one tree into another. Because of a combinatorial equivalence between binary trees and triangulations of convex polygons, rotation distance is equivalent to the flip distance for triangulations of convex polygons.