Definition
There are two definitions of hypergeometric terms, both used in different cases as explained below. See also hypergeometric series.
A term tk is a hypergeometric term if

is a rational function in k.
A term F(n,k) is a hypergeometric term if

is a rational function in k.
There exist two types of sums over hypergeometric terms, the definite and indefinite sums. A definite sum is of the form

The indefinite sum is of the form


In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function f is a differentiable function F whose derivative is equal to the original function f. This can be stated symbolically as F' = f. The process of solving for antiderivatives is called antidifferentiation, and its opposite operation is called differentiation, which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as F and G.
In mathematics, a series is, roughly speaking, an addition of infinitely many quantities, one after the other. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures through generating functions. The mathematical properties of infinite series make them widely applicable in other quantitative disciplines such as physics, computer science, statistics and finance.
In mathematics, a recurrence relation is an equation according to which the th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of ; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.

In analysis, numerical integration comprises a broad family of algorithms for calculating the numerical value of a definite integral. The term numerical quadrature is more or less a synonym for "numerical integration", especially as applied to one-dimensional integrals. Some authors refer to numerical integration over more than one dimension as cubature; others take "quadrature" to include higher-dimensional integration.
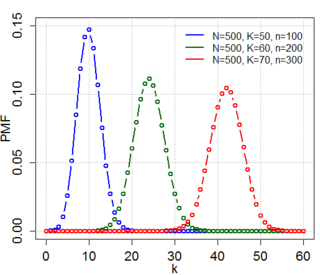
In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.
In symbolic computation, the Risch algorithm is a method of indefinite integration used in some computer algebra systems to find antiderivatives. It is named after the American mathematician Robert Henry Risch, a specialist in computer algebra who developed it in 1968.
In mathematics, a generalized hypergeometric series is a power series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by analytic continuation. The generalized hypergeometric series is sometimes just called the hypergeometric series, though this term also sometimes just refers to the Gaussian hypergeometric series. Generalized hypergeometric functions include the (Gaussian) hypergeometric function and the confluent hypergeometric function as special cases, which in turn have many particular special functions as special cases, such as elementary functions, Bessel functions, and the classical orthogonal polynomials.
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form where a0(x), ..., an(x) and b(x) are arbitrary differentiable functions that do not need to be linear, and y′, ..., y(n) are the successive derivatives of an unknown function y of the variable x.
In calculus, symbolic integration is the problem of finding a formula for the antiderivative, or indefinite integral, of a given function f(x), i.e. to find a formula for a differentiable function F(x) such that
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
In mathematics, basic hypergeometric series, or q-hypergeometric series, are q-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.
In mathematics, and more specifically in analysis, a holonomic function is a smooth function of several variables that is a solution of a system of linear homogeneous differential equations with polynomial coefficients and satisfies a suitable dimension condition in terms of D-modules theory. More precisely, a holonomic function is an element of a holonomic module of smooth functions. Holonomic functions can also be described as differentiably finite functions, also known as D-finite functions. When a power series in the variables is the Taylor expansion of a holonomic function, the sequence of its coefficients, in one or several indices, is also called holonomic. Holonomic sequences are also called P-recursive sequences: they are defined recursively by multivariate recurrences satisfied by the whole sequence and by suitable specializations of it. The situation simplifies in the univariate case: any univariate sequence that satisfies a linear homogeneous recurrence relation with polynomial coefficients, or equivalently a linear homogeneous difference equation with polynomial coefficients, is holonomic.
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration. Series acceleration techniques may also be used, for example, to obtain a variety of identities on special functions. Thus, the Euler transform applied to the hypergeometric series gives some of the classic, well-known hypergeometric series identities.
In mathematics, specifically combinatorics, a Wilf–Zeilberger pair, or WZ pair, is a pair of functions that can be used to certify certain combinatorial identities. WZ pairs are named after Herbert S. Wilf and Doron Zeilberger, and are instrumental in the evaluation of many sums involving binomial coefficients, factorials, and in general any hypergeometric series. A function's WZ counterpart may be used to find an equivalent and much simpler sum. Although finding WZ pairs by hand is impractical in most cases, Gosper's algorithm provides a method to find a function's WZ counterpart, and can be implemented in a symbolic manipulation program.
In mathematics, Gosper's algorithm, due to Bill Gosper, is a procedure for finding sums of hypergeometric terms that are themselves hypergeometric terms. That is: suppose one has a(1) + ... + a(n) = S(n) − S(0), where S(n) is a hypergeometric term (i.e., S(n + 1)/S(n) is a rational function of n); then necessarily a(n) is itself a hypergeometric term, and given the formula for a(n) Gosper's algorithm finds that for S(n).
In mathematics, Dixon's identity is any of several different but closely related identities proved by A. C. Dixon, some involving finite sums of products of three binomial coefficients, and some evaluating a hypergeometric sum. These identities famously follow from the MacMahon Master theorem, and can now be routinely proved by computer algorithms.

In mathematics, the Dyson conjecture is a conjecture about the constant term of certain Laurent polynomials, proved independently in 1962 by Wilson and Gunson. Andrews generalized it to the q-Dyson conjecture, proved by Zeilberger and Bressoud and sometimes called the Zeilberger–Bressoud theorem. Macdonald generalized it further to more general root systems with the Macdonald constant term conjecture, proved by Cherednik.
In discrete calculus the indefinite sum operator, denoted by or , is the linear operator, inverse of the forward difference operator . It relates to the forward difference operator as the indefinite integral relates to the derivative. Thus
Petkovšek's algorithm is a computer algebra algorithm that computes a basis of hypergeometric terms solution of its input linear recurrence equation with polynomial coefficients. Equivalently, it computes a first order right factor of linear difference operators with polynomial coefficients. This algorithm was developed by Marko Petkovšek in his PhD-thesis 1992. The algorithm is implemented in all the major computer algebra systems.
In mathematics a P-recursive equation is a linear equation of sequences where the coefficient sequences can be represented as polynomials. P-recursive equations are linear recurrence equations with polynomial coefficients. These equations play an important role in different areas of mathematics, specifically in combinatorics. The sequences which are solutions of these equations are called holonomic, P-recursive or D-finite.













