Related Research Articles
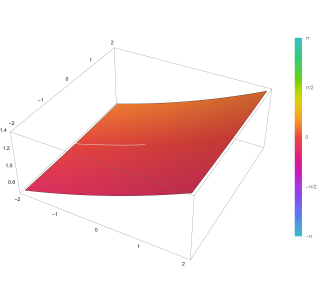
In mathematics, a generalized hypergeometric series is a power series in which the ratio of successive coefficients indexed by n is a rational function of n. The series, if convergent, defines a generalized hypergeometric function, which may then be defined over a wider domain of the argument by analytic continuation. The generalized hypergeometric series is sometimes just called the hypergeometric series, though this term also sometimes just refers to the Gaussian hypergeometric series. Generalized hypergeometric functions include the (Gaussian) hypergeometric function and the confluent hypergeometric function as special cases, which in turn have many particular special functions as special cases, such as elementary functions, Bessel functions, and the classical orthogonal polynomials.

In mathematics, a confluent hypergeometric function is a solution of a confluent hypergeometric equation, which is a degenerate form of a hypergeometric differential equation where two of the three regular singularities merge into an irregular singularity. The term confluent refers to the merging of singular points of families of differential equations; confluere is Latin for "to flow together". There are several common standard forms of confluent hypergeometric functions:
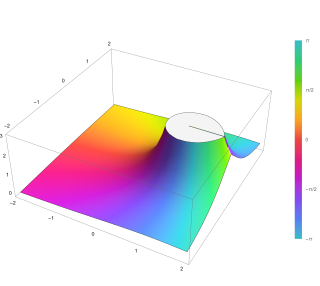
In mathematics, the Gaussian or ordinary hypergeometric function2F1(a,b;c;z) is a special function represented by the hypergeometric series, that includes many other special functions as specific or limiting cases. It is a solution of a second-order linear ordinary differential equation (ODE). Every second-order linear ODE with three regular singular points can be transformed into this equation.
In mathematics, basic hypergeometric series, or q-hypergeometric series, are q-analogue generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series. A series xn is called hypergeometric if the ratio of successive terms xn+1/xn is a rational function of n. If the ratio of successive terms is a rational function of qn, then the series is called a basic hypergeometric series. The number q is called the base.

Richard Allen Askey was an American mathematician, known for his expertise in the area of special functions. The Askey–Wilson polynomials are on the top level of the Askey scheme, which organizes orthogonal polynomials of hypergeometric type into a hierarchy. The Askey–Gasper inequality for Jacobi polynomials is essential in de Brange's famous proof of the Bieberbach conjecture.
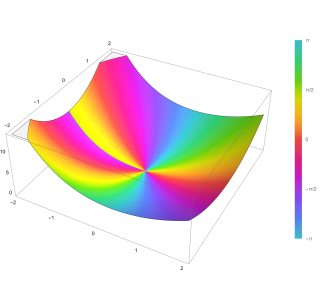
In mathematics, a Whittaker function is a special solution of Whittaker's equation, a modified form of the confluent hypergeometric equation introduced by Whittaker (1903) to make the formulas involving the solutions more symmetric. More generally, Jacquet (1966, 1967) introduced Whittaker functions of reductive groups over local fields, where the functions studied by Whittaker are essentially the case where the local field is the real numbers and the group is SL2(R).
Mary Celine Fasenmyer, RSM was an American mathematician and Catholic religious sister. She is most noted for her work on hypergeometric functions and linear algebra.
Lucy Joan Slater was a mathematician who worked on hypergeometric functions, and who found many generalizations of the Rogers–Ramanujan identities.
In mathematics, Clausen's formula, found by Thomas Clausen (1828), expresses the square of a Gaussian hypergeometric series as a generalized hypergeometric series. It states
In mathematics, Charlier polynomials are a family of orthogonal polynomials introduced by Carl Charlier. They are given in terms of the generalized hypergeometric function by
In mathematics, the q-Racah polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by Askey & Wilson (1979). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw give a detailed list of their properties.
In mathematics, a Barnes integral or Mellin–Barnes integral is a contour integral involving a product of gamma functions. They were introduced by Ernest William Barnes. They are closely related to generalized hypergeometric series.
In mathematics, a bilateral hypergeometric series is a series Σan summed over all integers n, and such that the ratio
In mathematics, an elliptic hypergeometric series is a series Σcn such that the ratio cn/cn−1 is an elliptic function of n, analogous to generalized hypergeometric series where the ratio is a rational function of n, and basic hypergeometric series where the ratio is a periodic function of the complex number n. They were introduced by Date-Jimbo-Kuniba-Miwa-Okado (1987) and Frenkel & Turaev (1997) in their study of elliptic 6-j symbols.

In the mathematical theory of special functions, Schwarz's list or the Schwartz table is the list of 15 cases found by Hermann Schwarz when hypergeometric functions can be expressed algebraically. More precisely, it is a listing of parameters determining the cases in which the hypergeometric equation has a finite monodromy group, or equivalently has two independent solutions that are algebraic functions. It lists 15 cases, divided up by the isomorphism class of the monodromy group, and was first derived by Schwarz by methods of complex analytic geometry. Correspondingly the statement is not directly in terms of the parameters specifying the hypergeometric equation, but in terms of quantities used to describe certain spherical triangles.

In mathematics, the continuous dual Hahn polynomials are a family of orthogonal polynomials in the Askey scheme of hypergeometric orthogonal polynomials. They are defined in terms of generalized hypergeometric functions by
In mathematics, the continuous q-Jacobi polynomialsP(α,β)
n(x|q), introduced by Askey & Wilson (1985), are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
In mathematics, the continuous big q-Hermite polynomials are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme. Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw give a detailed list of their properties.
In mathematics, the q-Laguerre polynomials, or generalized Stieltjes–Wigert polynomialsP(α)
n(x;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme introduced by Daniel S. Moak (1981). Roelof Koekoek, Peter A. Lesky, and René F. Swarttouw (2010, 14) give a detailed list of their properties.
Mikhail Kapranov, is a Russian mathematician, specializing in algebraic geometry, representation theory, mathematical physics, and category theory. He is currently a professor of the Kavli Institute for the Physics and Mathematics of the Universe at the University of Tokyo.
References
- Bailey, W. N. (1935), Generalized hypergeometric series, Cambridge Tracts in Mathematics and Mathematical Physics, No. 32, Cambridge University Press, MR 0185155
- Koepf, Wolfram (1995), "Algorithms for m-fold hypergeometric summation", Journal of Symbolic Computation, 20 (4): 399–417, doi: 10.1006/jsco.1995.1056 , ISSN 0747-7171, MR 1384455