
In mathematics, and more specifically in calculus, L'Hôpital's rule or L'Hospital's rule uses derivatives to help evaluate limits involving indeterminate forms. Application of the rule often converts an indeterminate form to an expression that can be evaluated by substitution, allowing easier evaluation of the limit. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the contribution of the rule is often attributed to L'Hôpital, the theorem was first introduced to L'Hôpital in 1694 by the Swiss mathematician Johann Bernoulli.

In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
The natural logarithm of a number is its logarithm to the base of the mathematical constant e, where e is an irrational and transcendental number approximately equal to 2.718281828459. The natural logarithm of x is generally written as ln x, logex, or sometimes, if the base e is implicit, simply log x. Parentheses are sometimes added for clarity, giving ln(x), loge(x) or log(x). This is done in particular when the argument to the logarithm is not a single symbol, to prevent ambiguity.

In mathematics, the Dirac delta function is a generalized function or distribution introduced by the physicist Paul Dirac. It is used to model the density of an idealized point mass or point charge as a function equal to zero everywhere except for zero and whose integral over the entire real line is equal to one. As there is no function that has these properties, the computations made by the theoretical physicists appeared to mathematicians as nonsense until the introduction of distributions by Laurent Schwartz to formalize and validate the computations. As a distribution, the Dirac delta function is a linear functional that maps every function to its value at zero. The Kronecker delta function, which is usually defined on a discrete domain and takes values 0 and 1, is a discrete analog of the Dirac delta function.

In probability theory, a log-normal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed. Thus, if the random variable X is log-normally distributed, then Y = ln(X) has a normal distribution. Likewise, if Y has a normal distribution, then the exponential function of Y, X = exp(Y), has a log-normal distribution. A random variable which is log-normally distributed takes only positive real values. The distribution is occasionally referred to as the Galton distribution or Galton's distribution, after Francis Galton. The log-normal distribution also has been associated with other names, such as McAlister, Gibrat and Cobb–Douglas.
In calculus, and more generally in mathematical analysis, integration by parts or partial integration is a process that finds the integral of a product of functions in terms of the integral of their derivative and antiderivative. It is frequently used to transform the antiderivative of a product of functions into an antiderivative for which a solution can be more easily found. The rule can be readily derived by integrating the product rule of differentiation.

In mathematics, the inverse trigonometric functions are the inverse functions of the trigonometric functions. Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, and are used to obtain an angle from any of the angle's trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.
In mathematics, Laplace's method, named after Pierre-Simon Laplace, is a technique used to approximate integrals of the form

In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be stable if its distribution is stable. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
In mathematical physics, a Grassmann integral, or, more correctly, Berezin integral, is a way to define integration for functions of Grassmann variables. It is not an integral in the Lebesgue sense; it is called integration because it has analogous properties and since it is used in physics as a sum over histories for fermions, an extension of the path integral. The technique was invented by the Russian mathematician Felix Berezin and developed in his textbook. Some earlier insights were made by the physicist David John Candlin in 1956.
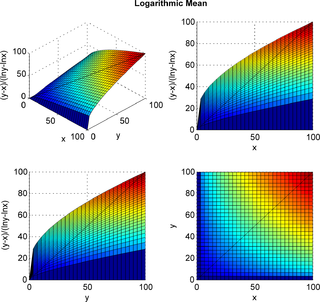
In mathematics, the logarithmic mean is a function of two non-negative numbers which is equal to their difference divided by the logarithm of their quotient. This calculation is applicable in engineering problems involving heat and mass transfer.
Expected shortfall (ES) is a risk measure—a concept used in the field of financial risk measurement to evaluate the market risk or credit risk of a portfolio. The "expected shortfall at q% level" is the expected return on the portfolio in the worst % of cases. ES is an alternative to value at risk that is more sensitive to the shape of the tail of the loss distribution.
In classical mechanics, a Liouville dynamical system is an exactly soluble dynamical system in which the kinetic energy T and potential energy V can be expressed in terms of the s generalized coordinates q as follows:

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.
There are common integrals in quantum field theory that appear repeatedly. These integrals are all variations and generalizations of gaussian integrals to the complex plane and to multiple dimensions. Other integrals can be approximated by versions of the gaussian integral. Fourier integrals are also considered.
In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativisic velocity addition formula.

In fluid dynamics, a cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength, as compared to the water depth.
Uncertainty theory is a branch of mathematics based on normality, monotonicity, self-duality, countable subadditivity, and product measure axioms. It was founded by Baoding Liu in 2007 and refined in 2009.
In image analysis, the generalized structure tensor (GST) is an extension of the Cartesian structure tensor to curvilinear coordinates.. It is mainly used to detect and to represent the "direction" parameters of curves, just as the Cartesian structure tensor detects and represents the direction in Cartesian coordinates. Curve families generated by pairs of locally orthogonal functions have been the best studied.













