
In the theory of computation, a branch of theoretical computer science, a pushdown automaton (PDA) is a type of automaton that employs a stack.

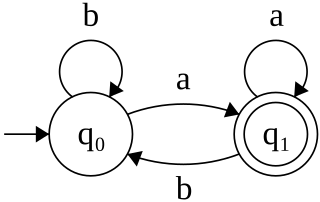
Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science with close connections to mathematical logic. The word automata comes from the Greek word αὐτόματος, which means "self-acting, self-willed, self-moving". An automaton is an abstract self-propelled computing device which follows a predetermined sequence of operations automatically. An automaton with a finite number of states is called a Finite Automaton (FA) or Finite-State Machine (FSM). The figure on the right illustrates a finite-state machine, which is a well-known type of automaton. This automaton consists of states and transitions. As the automaton sees a symbol of input, it makes a transition to another state, according to its transition function, which takes the previous state and current input symbol as its arguments.
In computer science and automata theory, a deterministic Büchi automaton is a theoretical machine which either accepts or rejects infinite inputs. Such a machine has a set of states and a transition function, which determines which state the machine should move to from its current state when it reads the next input character. Some states are accepting states and one state is the start state. The machine accepts an input if and only if it will pass through an accepting state infinitely many times as it reads the input.

In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton (DFA)—also known as deterministic finite acceptor (DFA), deterministic finite-state machine (DFSM), or deterministic finite-state automaton (DFSA)—is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. Deterministic refers to the uniqueness of the computation run. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.
In automata theory, a finite-state machine is called a deterministic finite automaton (DFA), if
In automata theory, an alternating finite automaton (AFA) is a nondeterministic finite automaton whose transitions are divided into existential and universal transitions. For example, let A be an alternating automaton.
A finite-state transducer (FST) is a finite-state machine with two memory tapes, following the terminology for Turing machines: an input tape and an output tape. This contrasts with an ordinary finite-state automaton, which has a single tape. An FST is a type of finite-state automaton (FSA) that maps between two sets of symbols. An FST is more general than an FSA. An FSA defines a formal language by defining a set of accepted strings, while an FST defines a relation between sets of strings.
In the theory of computation and automata theory, the powerset construction or subset construction is a standard method for converting a nondeterministic finite automaton (NFA) into a deterministic finite automaton (DFA) which recognizes the same formal language. It is important in theory because it establishes that NFAs, despite their additional flexibility, are unable to recognize any language that cannot be recognized by some DFA. It is also important in practice for converting easier-to-construct NFAs into more efficiently executable DFAs. However, if the NFA has n states, the resulting DFA may have up to 2n states, an exponentially larger number, which sometimes makes the construction impractical for large NFAs.
In automata theory, a deterministic pushdown automaton is a variation of the pushdown automaton. The class of deterministic pushdown automata accepts the deterministic context-free languages, a proper subset of context-free languages.
In computer science, in particular in automata theory, a two-way finite automaton is a finite automaton that is allowed to re-read its input.
In automata theory, a Muller automaton is a type of an ω-automaton. The acceptance condition separates a Muller automaton from other ω-automata. The Muller automaton is defined using a Muller acceptance condition, i.e. the set of all states visited infinitely often must be an element of the acceptance set. Both deterministic and non-deterministic Muller automata recognize the ω-regular languages. They are named after David E. Muller, an American mathematician and computer scientist, who invented them in 1963.
In mathematics and computer science, the probabilistic automaton (PA) is a generalization of the nondeterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix. Thus, the probabilistic automaton also generalizes the concepts of a Markov chain and of a subshift of finite type. The languages recognized by probabilistic automata are called stochastic languages; these include the regular languages as a subset. The number of stochastic languages is uncountable.
A read-only Turing machine or two-way deterministic finite-state automaton (2DFA) is class of models of computability that behave like a standard Turing machine and can move in both directions across input, except cannot write to its input tape. The machine in its bare form is equivalent to a deterministic finite automaton in computational power, and therefore can only parse a regular language.
A tree-walking automaton (TWA) is a type of finite automaton that deals with tree structures rather than strings. The concept was originally proposed by Aho and Ullman.
In computer science, more specifically in automata and formal language theory, nested words are a concept proposed by Alur and Madhusudan as a joint generalization of words, as traditionally used for modelling linearly ordered structures, and of ordered unranked trees, as traditionally used for modelling hierarchical structures. Finite-state acceptors for nested words, so-called nested word automata, then give a more expressive generalization of finite automata on words. The linear encodings of languages accepted by finite nested word automata gives the class of visibly pushdown languages. The latter language class lies properly between the regular languages and the deterministic context-free languages. Since their introduction in 2004, these concepts have triggered much research in that area.
In automata theory, a branch of theoretical computer science, an ω-automaton is a variation of a finite automaton that runs on infinite, rather than finite, strings as input. Since ω-automata do not stop, they have a variety of acceptance conditions rather than simply a set of accepting states.
In automata theory, a semi-deterministic Büchi automaton is a special type of Büchi automaton. In such an automaton, the set of states can be partitioned into two subsets: one subset forms a deterministic automaton and also contains all the accepting states.
In automata theory, a generalized Büchi automaton is a variant of a Büchi automaton. The difference with the Büchi automaton is the accepting condition, which is determined by a set of sets of states. A run is accepted by the automaton if it visits at least one state of every set of the accepting condition infinitely often. Generalized Büchi automata are equivalent in expressive power to Büchi automata; a transformation is given here.
In automata theory, a co-Büchi automaton is a variant of Büchi automaton. The only difference is the accepting condition: a Co-Büchi automaton accepts an infinite word if there exists a run, such that all the states occurring infinitely often in the run are in the final state set . In contrast, a Büchi automaton accepts a word if there exists a run, such that at least one state occurring infinitely often in the final state set .
In theoretical computer science and formal language theory, a weighted automaton or weighted finite-state machine is a generalization of a finite-state machine in which the edges have weights, for example real numbers or integers. Finite-state machines are only capable of answering decision problems; they take as input a string and produce a Boolean output, i.e. either "accept" or "reject". In contrast, weighted automata produce a quantitative output, for example a count of how many answers are possible on a given input string, or a probability of how likely the input string is according to a probability distribution. They are one of the simplest studied models of quantitative automata.






































