Input enhancement (computer science)

Last updated November 02, 2023

In computer science, input enhancement is the principle that processing a given input to a problem and altering it in a specific way will increase runtime efficiency or space efficiency, or both. The altered input is usually stored and accessed to simplify the problem. By exploiting the structure and properties of the inputs, input enhancement creates various speed-ups in the efficiency of the algorithm.

Searching

Input enhancement when searching has been an essential component of the algorithm world for some time in computer science. The main idea behind this principle is that the efficiency of a search is much faster when the time is taken to create or sort a data structure of the given input before attempting to search for the element in said data structure.

Presorting

Presorting is the technique of sorting an input before attempting to search it. Because the addition of a sorting component to an algorithm is added to the runtime of the searching algorithm, and not multiplied, it only competes for the slowest portion of the algorithm. Since the efficiency of algorithms is measured by the slowest component, the addition of the sorting component is negligible if the search is less efficient. Unfortunately, presorting is usually the slowest component of the algorithm. Contrasting, a searching algorithm without a presort is almost always slower than that with a presort.

The sorting portion of the algorithm processes the input of the problem before the searching portion of the algorithm is even reached. Having the elements of the input sorted in some sort of order makes the search trivial in practice. The simplest sorting algorithms – insertion sort, selection sort, and bubble sort – all have a worst case runtime of O(n²), while the more advanced sorting algorithms – heapsort, merge sort – which have a worst case runtime of O(n log n) – and quicksort – which has a worst case of O(n²) but is almost always O(n log n). Utilizing these sorting algorithms, a search algorithm that incorporates presorting will yield these big-O efficiencies.

A simple example of the benefits of presorting can be seen with an algorithm that checks an array for unique elements: If an array of n elements is given, return true if every element in the array is unique, otherwise return false. The pseudocode is presented below:

algorithm uniqueElementSearch(A[0...n]) isfori := 0 ton – 1 doforj := i + 1 tondoif A[i] = A[j] thenreturn falsereturn true

Without a presort, at worst case, this algorithm would require every element to be checked against every other element with two possible outcomes: either there is no duplicate element in the array, or the last two elements in the array are the duplicates. This results in an O(n²) efficiency.

Now compare this to a similar algorithm that utilizes presorting. This algorithm sorts the inputted array, and then checks each pair of elements for a duplicate. The pseudocode is presented below:

algorithm presortUniqueElementSearch(A[0...n]) is     sort(A[0...n])     fori := 0 ton – 1 doif A[i] = A[i + 1] thenreturn falsereturn true

As previously stated, the least efficient part of this algorithm is the sorting of the array, which, if an efficient sort is selected, would run in O(n log n). But after the array is sorted, the array only needs to be traversed once, which would run in O(n). This results in an O(n log n) efficiency.

This simple example demonstrates what is capable with an input enhancement technique such as presorting. The algorithm went from quadratic runtime to linearithmic runtime which will result in speed-ups for large inputs.

In trees

Creating data structures to more efficiently search through data is also a form of input enhancement. Placing data into a tree to store and search through inputs is another popular technique. Trees are used throughout computer science and many different types of trees – binary search trees, AVL trees, red–black trees, and 2–3 trees to name just a small few – have been developed to properly store, access, and manipulate data while maintaining their structure. Trees are a principal data structure for dictionary implementation.

The benefits of putting data in a tree are great, especially if the data is being manipulated or repeatedly searched through. Binary search trees are the most simplest, yet most common type of tree for this implementation. The insertion, deletion, and searching of items in a tree are all worst case O(n), but are most often executed in O(log n). This makes the repeated searching of elements even quicker for large inputs. There are many different types of binary search trees that work more efficiently and even self-balance upon addition and removal of items, like the AVL tree which has a worst case O(log n) for all searching, inserting, and deletion.

Taking the time to put the inputted data into such a structure will have great speed-ups for repeated searching of elements, as opposed to searching through the data that hasn't enhanced.

String matching

String matching is a complex issue in the world of programming now that search engines are the forefront of the internet and the online world. When given a keyword or a string that needs to be searched among millions upon millions of words, it would take an unbelievable amount of time to match this string character per character. Input enhancement allows an input to be altered to make this process that much faster.

The brute-force algorithm for this problem would perform as follows: When presented with a string of n characters, often called the key or pattern, the string would be compared to every single character of a longer string m, often called the text. If a matched character occurs, it checks the second character of the key to see if it matches. If it does, the next character is checked and so on until the string matches or the subsequent character doesn't match and the entire key shifts a single character. This continues until the key is found or until the text is exhausted.

This algorithm is extremely inefficient. The maximum number of check trials would be m-n+1 trials, making the big-O efficiency at worst case O(mn). On average case, the maximum number of check trials would never be reached and only a few would be executed, resulting in an average time efficiency of O(m+n).

Because of the necessity of more efficient string matching algorithms, several faster algorithms have been developed, with most of them utilizing the idea of input enhancement. The key is preprocessed to gather information about what to look for in the text and that information is stored in order to refer back to them when necessary. The accessing of this information is constant time and greatly increases the runtime efficiency of the algorithms that use it, most famously the Knuth–Morris–Pratt algorithm and the Boyer–Moore algorithm. These algorithms, for the most part, use the same methods to obtain its efficiency with the main difference being on how the key is composed.

Horspool's algorithm

As a demonstration of input enhancement in string matching, one should examine a simplified version of the Boyer-Moore algorithm, Horspool's algorithm. The algorithm starts at the nth character of the text m and compares the character. Let's call this character x. There are 4 possible cases of what can happen next.

Case 1: The first possible case is that the character x is not in the key. If this occurs, the entire key can be shifted the length of the key.

Case 2: The second possible case is that the character x is not the current character, but x is in the key. If this occurs, the key is shifted to align the rightmost occurrence of the character x.

Case 3: The third possible case is that the character x matches with the last character in the key but the other characters don't fully match the key and x doesn't occur again in the key. If this occurs, the entire key can be shifted the length of the key.

Case 4: The fourth and last possible case is that character x matches the key but the other characters don't fully match the key and x does occur again in the key. If this occurs, the key is shifted to align the rightmost occurrence if the character x.

This may seem like it is not more efficient than the brute-force algorithm since it has to check all of the characters on every check. However, this is not the case. Horspool's algorithm utilizes a shift table to store the number of characters the algorithm should shift if it runs into a specific character. The input is precomputed into a table with every possible character that can be encountered in the text. The shift size is computed with two options: one, if the character is in not in the key, then the shift size is n, the length of the key; or two, if the character appears in the key, then its shift value is the distance from the rightmost occurrence of the character in the first n-1 characters in the key. The algorithm for the shift table generator is given the key and an alphabet of possible characters that could appear in the string (K[0...n-1]) as input and returns the shift table (T[0...s-1]). Pseudocode for the shift table generator and an example of the shift table for the string ‘POTATO’ is displayed below:

algorithm shiftTableGenerator(K[0...n-1]) isfori = 0 tos – 1 do         T[i] := mforj := 0 ton – 2 do                 T[P[j]] := n – 1 – jreturn T

Shift Table for 'POTATO'
character x	A	B	C	...	O	P	...	T	...	Z	_
shift value	2	6	6	6	4	5	6	1	6	6	6

After the shift table is constructed in the input enhancement stage, the algorithm lines up the key and starts executing. The algorithm executes until a matching substring of text m is found or the key overlaps the last characters of text m. If the algorithm encounters a pair of characters that do not match, it accesses the table for the character's shift value and shifts accordingly. Horspool's algorithm takes the key (K[0...n-1]) and the text (M[0...m-1]) and outputs either the index of the matching substring or the string “Key not found” depending on the result. Pseudocode for Horspool's algorithm is presented below:

algorithm HorspoolsAlgorithm(K[0...n-1]), M[0...m-1]) is     shiftTableGenerator(K[0...n-1])     i := n – 1     whilei ≤ m – 1 dok := 0         whilek ≤ m – 1 and K[n – 1 – k] = M[i – k] dok := k + 1             ifk = mthenreturni – n + 1             elsei = i + T[M[i]]     return “Key not found”

Although it may not be evident, the worst case runtime efficiency of this algorithm is O(mn). Fortunately, on texts that are random, the runtime efficiency is linear, O(n/m). This places Horspool's algorithm, which utilizes input enhancement, in a much faster class than the brute-force algorithm for this problem.

Related concepts

Input enhancement is often used interchangeably with precomputation and preprocessing. Although they are related, there are several important differences that must be noted.

Precomputing and input enhancement can sometimes be used synonymously. More specifically, precomputation is the calculation of a given input before anything else is done to the input. Oftentimes a table is generated to be looked back on during the actual execution of the algorithm. Input enhancement that calculates values and assigns them to elements of the input can be classified as precomputation, but the similarities stop there. There are sections of input enhancement that do not utilize precomputing and the terms should not be mutually used.
When speaking about altering inputs, preprocessing is often misused. In computer science, a preprocessor and preprocessing are entirely different. When preprocessing is used in context, the usual intention is to portray the concept of input enhancement, and not that of utilizing a preprocessor. Implementing a preprocessor is the concept in which a program takes an input and processes it into an output to be used by another program entirely. This sounds like input enhancement, but the application of preprocessor applies to the generic program that processes the source input to be outputted in a format that a compiler can read and can then be compiled.

Related Research Articles

In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the middle element of the array. If they are not equal, the half in which the target cannot lie is eliminated and the search continues on the remaining half, again taking the middle element to compare to the target value, and repeating this until the target value is found. If the search ends with the remaining half being empty, the target is not in the array.

A hash function is any function that can be used to map data of arbitrary size to fixed-size values, though there are some hash functions that support variable length output. The values returned by a hash function are called hash values, hash codes, digests, or simply hashes. The values are usually used to index a fixed-size table called a hash table. Use of a hash function to index a hash table is called hashing or scatter storage addressing.

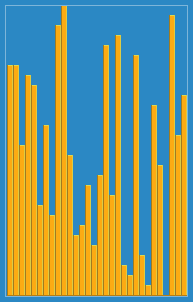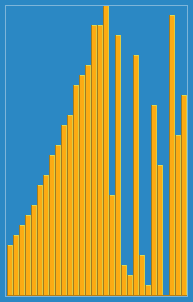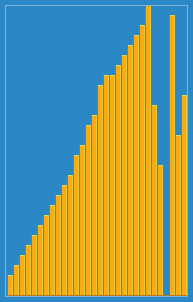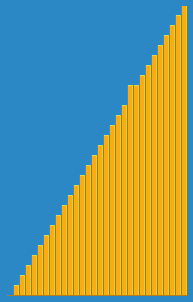
<span class="mw-page-title-main">Insertion sort</span> Sorting algorithm

Insertion sort is a simple sorting algorithm that builds the final sorted array (or list) one item at a time by comparisons. It is much less efficient on large lists than more advanced algorithms such as quicksort, heapsort, or merge sort. However, insertion sort provides several advantages:

<span class="mw-page-title-main">Sorting algorithm</span> Algorithm that arranges lists in order

In computer science, a sorting algorithm is an algorithm that puts elements of a list into an order. The most frequently used orders are numerical order and lexicographical order, and either ascending or descending. Efficient sorting is important for optimizing the efficiency of other algorithms that require input data to be in sorted lists. Sorting is also often useful for canonicalizing data and for producing human-readable output.

In computer science, string-searching algorithms, sometimes called string-matching algorithms, are an important class of string algorithms that try to find a place where one or several strings are found within a larger string or text.

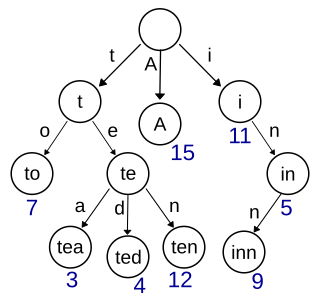
In computer science, a trie, also called digital tree or prefix tree, is a type of k-ary search tree, a tree data structure used for locating specific keys from within a set. These keys are most often strings, with links between nodes defined not by the entire key, but by individual characters. In order to access a key, the trie is traversed depth-first, following the links between nodes, which represent each character in the key.

In computer science, the Knuth–Morris–Pratt algorithm is a string-searching algorithm that searches for occurrences of a "word" W within a main "text string" S by employing the observation that when a mismatch occurs, the word itself embodies sufficient information to determine where the next match could begin, thus bypassing re-examination of previously matched characters.

In computer science, the Boyer–Moore string-search algorithm is an efficient string-searching algorithm that is the standard benchmark for practical string-search literature. It was developed by Robert S. Boyer and J Strother Moore in 1977. The original paper contained static tables for computing the pattern shifts without an explanation of how to produce them. The algorithm for producing the tables was published in a follow-on paper; this paper contained errors which were later corrected by Wojciech Rytter in 1980.

In computer science, a suffix tree is a compressed trie containing all the suffixes of the given text as their keys and positions in the text as their values. Suffix trees allow particularly fast implementations of many important string operations.

In computer science, a fusion tree is a type of tree data structure that implements an associative array on $w$ -bit integers on a finite universe, where each of the input integers has size less than 2^w and is non-negative. When operating on a collection of $n$ key–value pairs, it uses $O (n)$ space and performs searches in $O (log w n)$ time, which is asymptotically faster than a traditional self-balancing binary search tree, and also better than the van Emde Boas tree for large values of $w$ . It achieves this speed by using certain constant-time operations that can be done on a machine word. Fusion trees were invented in 1990 by Michael Fredman and Dan Willard.

In computer science, a suffix array is a sorted array of all suffixes of a string. It is a data structure used in, among others, full-text indices, data-compression algorithms, and the field of bibliometrics.

In computer science, a radix tree is a data structure that represents a space-optimized trie in which each node that is the only child is merged with its parent. The result is that the number of children of every internal node is at most the radix $r$ of the radix tree, where $r$ is a positive integer and a power $x$ of 2, having $x$ ≥ 1. Unlike regular trees, edges can be labeled with sequences of elements as well as single elements. This makes radix trees much more efficient for small sets and for sets of strings that share long prefixes.

<i>k</i>-d tree Multidimensional search tree for points in k dimensional space

In computer science, a k-d tree is a space-partitioning data structure for organizing points in a k-dimensional space. K-dimensional is that which concerns exactly k orthogonal axes or a space of any number of dimensions. k-d trees are a useful data structure for several applications, such as:

In computer science, the Boyer–Moore–Horspool algorithm or Horspool's algorithm is an algorithm for finding substrings in strings. It was published by Nigel Horspool in 1980 as SBM.

Spreadsort is a sorting algorithm invented by Steven J. Ross in 2002. It combines concepts from distribution-based sorts, such as radix sort and bucket sort, with partitioning concepts from comparison sorts such as quicksort and mergesort. In experimental results it was shown to be highly efficient, often outperforming traditional algorithms such as quicksort, particularly on distributions exhibiting structure and string sorting. There is an open-source implementation with performance analysis and benchmarks, and HTML documentation .

In computer science, the Commentz-Walter algorithm is a string searching algorithm invented by Beate Commentz-Walter. Like the Aho–Corasick string matching algorithm, it can search for multiple patterns at once. It combines ideas from Aho–Corasick with the fast matching of the Boyer–Moore string-search algorithm. For a text of length n and maximum pattern length of m, its worst-case running time is O(mn), though the average case is often much better.

In computer science, the longest common prefix array is an auxiliary data structure to the suffix array. It stores the lengths of the longest common prefixes (LCPs) between all pairs of consecutive suffixes in a sorted suffix array.

In computer science, the Raita algorithm is a string searching algorithm which improves the performance of Boyer–Moore–Horspool algorithm. This algorithm preprocesses the string being searched for the pattern, which is similar to Boyer–Moore string-search algorithm. The searching pattern of particular sub-string in a given string is different from Boyer–Moore–Horspool algorithm. This algorithm was published by Timo Raita in 1991.

In computer science, a generalized suffix array (or GSA) is a suffix array containing all suffixes for a set of strings. Given the set of strings $of total length, it is a lexicographically sorted array of all suffixes of each string in . It is primarily used in bioinformatics and string processing.$

References

Levitin, Anany (2012). Introduction to The Design & Analysis of Algorithms (Third Edition). Pearson. ISBN 978-0-13-231681-1
Sebesta, Robert W. (2012). Concepts of Programming Languages (Tenth Edition). Pearson. ISBN 978-0-13-139531-2

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.