Interpolative decomposition

Last updated April 09, 2019

In numerical analysis interpolative decomposition (ID) factors a matrix as the product of two matrices, one of which contains selected columns from the original matrix, and the other has a subset of columns that consists the identity matrix and all its values are not larger than 2 in absolute value.

Numerical analysis study of algorithms that use numerical approximation for the problems of mathematical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis. Numerical analysis naturally finds application in all fields of engineering and the physical sciences, but in the 21st century also the life sciences, social sciences, medicine, business and even the arts have adopted elements of scientific computations. As an aspect of mathematics and computer science that generates, analyzes, and implements algorithms, the growth in power and the revolution in computing has raised the use of realistic mathematical models in science and engineering, and complex numerical analysis is required to provide solutions to these more involved models of the world. Ordinary differential equations appear in celestial mechanics ; numerical linear algebra is important for data analysis; stochastic differential equations and Markov chains are essential in simulating living cells for medicine and biology.

Matrix (mathematics) Two-dimensional array of numbers with specific operations

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimensions of the matrix below are 2 × 3, because there are two rows and three columns:

In linear algebra, the identity matrix, or sometimes ambiguously called a unit matrix, of size n is the n × n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by I_n, or simply by I if the size is immaterial or can be trivially determined by the context. Less frequently, some mathematics books use U or E to represent the identity matrix, meaning "unit matrix" and the German word "Einheitsmatrix", respectively.

Definition

Let $A$ be an $m\times n$ matrix with rank $r$ . The matrix $A$ can be written as:

In linear algebra, the rank of a matrix $is the dimension of the vector space generated by its columns. This corresponds to the maximal number of linearly independent columns of . This, in turn, is identical to the dimension of the space spanned by its rows. Rank is thus a measure of the "nondegenerateness" of the system of linear equations and linear transformation encoded by . There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics.$

A=A_{(:,J)}X,\,

where:

$J$ is a subset of $r$ indices from $1,\ldots ,n$
The $m\times r$ matrix $A_{(:,J)}$ represents the $J$ 's columns of $A$
$X$ is a $r\times n$ matrix that all its values are less than 2 in magnitude. $X$ has a $r\times r$ identity sub-matrix.

Note that similar decomposition can be done using the rows of $A$ .

Example

Let $A$ be the $3\times 3$ matrix of rank 2: $A={\begin{bmatrix}34&58&52\\59&89&80\\17&29&26\end{bmatrix}}$

If $J={\begin{bmatrix}2&1&3\end{bmatrix}}$ , then

A={\begin{bmatrix}58&34\\89&59\\29&17\end{bmatrix}}{\begin{bmatrix}0&1&0.8788\\1&0&0.0303\end{bmatrix}}

Notes

Related Research Articles

In linear algebra, the determinant is a scalar value that can be computed from the elements of a square matrix and encodes certain properties of the linear transformation described by the matrix. The determinant of a matrix $A$ is denoted $det(A)$ , $det A$ , or $| A |$ . Geometrically, it can be viewed as the volume scaling factor of the linear transformation described by the matrix. This is also the signed volume of the n-dimensional parallelepiped spanned by the column or row vectors of the matrix. The determinant is positive or negative according to whether the linear mapping preserves or reverses the orientation of n-space.

In linear algebra, a symmetric $real matrix is said to be positive definite if the scalar is strictly positive for every non-zero column vector of real numbers. Here denotes the transpose of .. When interpreting as the output of an operator,, that is acting on an input,, the property of positive definiteness implies that the output always has a positive inner product with the input, as often observed in physical processes.$

In linear algebra, the column space of a matrix A is the span of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.

An orthogonal matrix is a square matrix whose columns and rows are orthogonal unit vectors, i.e.

In mathematics, matrix multiplication or matrix product is a binary operation that produces a matrix from two matrices with entries in a field, or, more generally, in a ring or even a semiring. The matrix product is designed for representing the composition of linear maps that are represented by matrices. Matrix multiplication is thus a basic tool of linear algebra, and as such has numerous applications in many areas of mathematics, as well as in applied mathematics, statistics, physics, economics, and engineering. In more detail, if $A$ is an $n \times m$ matrix and $B$ is an $m \times p$ matrix, their matrix product $AB$ is an $n \times p$ matrix, in which the $m$ entries across a row of $A$ are multiplied with the $m$ entries down a column of $B$ and summed to produce an entry of $AB$ . When two linear maps are represented by matrices, then the matrix product represents the composition of the two maps.

In mathematics, a square matrix is a matrix with the same number of rows and columns. An n-by-n matrix is known as a square matrix of order n. Any two square matrices of the same order can be added and multiplied.

In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The term usually refers to square matrices. An example of a 2-by-2 diagonal matrix is $; the following matrix is a 3-by-3 diagonal matrix: . An identity matrix of any size, or any multiple of it, will be a diagonal matrix.$

In linear algebra, an n-by-n square matrix A is called invertible if there exists an n-by-n square matrix B such that

In mathematics applied to computer science, Monge arrays, or Monge matrices, are mathematical objects named for their discoverer, the French mathematician Gaspard Monge.

In mathematics, particularly in matrix theory, a permutation matrix is a square binary matrix that has exactly one entry of 1 in each row and each column and 0s elsewhere. Each such matrix, say $P$ , represents a permutation of $m$ elements and, when used to multiply another matrix, say $A$ , results in permuting the rows or columns of the matrix $A$ .

In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A = QR of an orthogonal matrix Q and an upper triangular matrix R. QR decomposition is often used to solve the linear least squares problem and is the basis for a particular eigenvalue algorithm, the QR algorithm.

In abstract algebra, a matrix ring is any collection of matrices over some ring R that form a ring under matrix addition and matrix multiplication. The set of n × n matrices with entries from R is a matrix ring denoted M_n(R), as well as some subsets of infinite matrices which form infinite matrix rings. Any subring of a matrix ring is a matrix ring.

In linear algebra, linear transformations can be represented by matrices. If $is a linear transformation mapping to and is a column vector with entries, then$

In mathematics, the Smith normal form is a normal form that can be defined for any matrix with entries in a principal ideal domain (PID). The Smith normal form of a matrix is diagonal, and can be obtained from the original matrix by multiplying on the left and right by invertible square matrices. In particular, the integers are a PID, so one can always calculate the Smith normal form of an integer matrix. The Smith normal form is very useful for working with finitely generated modules over a PID, and in particular for deducing the structure of a quotient of a free module. It is named for the British mathematician Henry John Stephen Smith.

In mathematics, and in particular, algebra, a generalized inverse of an element x is an element y that has some properties of an inverse element but not necessarily all of them. Generalized inverses can be defined in any mathematical structure that involves associative multiplication, that is, in a semigroup. This article describes generalized inverses of a matrix $.$

In mathematics, especially in linear algebra and matrix theory, the vectorization of a matrix is a linear transformation which converts the matrix into a column vector. Specifically, the vectorization of an m × n matrix A, denoted vec(A), is the mn × 1 column vector obtained by stacking the columns of the matrix A on top of one another:

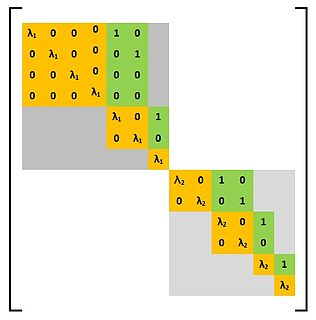
In mathematics, in linear algebra, a Weyr canonical form is a square matrix satisfying certain conditions. A square matrix is said to be in the Weyr canonical form if the matrix satisfies the conditions defining the Weyr canonical form. The Weyr form was discovered by the Czech mathematician Eduard Weyr in 1885. The Weyr form did not become popular among mathematicians and it was overshadowed by the closely related, but distinct, canonical form known by the name Jordan canonical form. The Weyr form has been rediscovered several times since Weyr’s original discovery in 1885. This form has been variously called as modified Jordan form,reordered Jordan form,second Jordan form, and H-form. The current terminology is credited to Shapiro who introduced it in a paper published in the American Mathematical Monthly in 1999.

References

Cheng, Hongwei, Zydrunas Gimbutas, Per-Gunnar Martinsson, and Vladimir Rokhlin. "On the compression of low rank matrices." SIAM Journal on Scientific Computing 26, no. 4 (2005): 1389–1404.
Liberty, E., Woolfe, F., Martinsson, P. G., Rokhlin, V., & Tygert, M. (2007). Randomized algorithms for the low-rank approximation of matrices. Proceedings of the National Academy of Sciences, 104(51), 20167–20172.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.