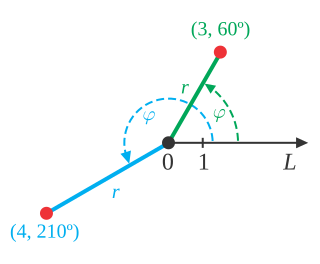
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are

In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.
In Einstein's theory of general relativity, the Schwarzschild metric is an exact solution to the Einstein field equations that describes the gravitational field outside a spherical mass, on the assumption that the electric charge of the mass, angular momentum of the mass, and universal cosmological constant are all zero. The solution is a useful approximation for describing slowly rotating astronomical objects such as many stars and planets, including Earth and the Sun. It was found by Karl Schwarzschild in 1916.
In general relativity, Eddington–Finkelstein coordinates are a pair of coordinate systems for a Schwarzschild geometry which are adapted to radial null geodesics. Null geodesics are the worldlines of photons; radial ones are those that are moving directly towards or away from the central mass. They are named for Arthur Stanley Eddington and David Finkelstein. Although they appear to have inspired the idea, neither ever wrote down these coordinates or the metric in these coordinates. Roger Penrose seems to have been the first to write down the null form but credits it to the above paper by Finkelstein, and, in his Adams Prize essay later that year, to Eddington and Finkelstein. Most influentially, Misner, Thorne and Wheeler, in their book Gravitation, refer to the null coordinates by that name.
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.
The Kerr metric or Kerr geometry describes the geometry of empty spacetime around a rotating uncharged axially symmetric black hole with a quasispherical event horizon. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which makes exact solutions very difficult to find.
In physics and astronomy, the Reissner–Nordström metric is a static solution to the Einstein–Maxwell field equations, which corresponds to the gravitational field of a charged, non-rotating, spherically symmetric body of mass M. The analogous solution for a charged, rotating body is given by the Kerr–Newman metric.
The Schwarzschild solution describes spacetime under the influence of a massive, non-rotating, spherically symmetric object. It is considered by some to be one of the simplest and most useful solutions to the Einstein field equations.
In physics, spherically symmetric spacetimes are commonly used to obtain analytic and numerical solutions to Einstein's field equations in the presence of radially moving matter or energy. Because spherically symmetric spacetimes are by definition irrotational, they are not realistic models of black holes in nature. However, their metrics are considerably simpler than those of rotating spacetimes, making them much easier to analyze.
A frame field in general relativity is a set of four pointwise-orthonormal vector fields, one timelike and three spacelike, defined on a Lorentzian manifold that is physically interpreted as a model of spacetime. The timelike unit vector field is often denoted by and the three spacelike unit vector fields by . All tensorial quantities defined on the manifold can be expressed using the frame field and its dual coframe field.
In theoretical physics, Nordström's theory of gravitation was a predecessor of general relativity. Strictly speaking, there were actually two distinct theories proposed by the Finnish theoretical physicist Gunnar Nordström, in 1912 and 1913 respectively. The first was quickly dismissed, but the second became the first known example of a metric theory of gravitation, in which the effects of gravitation are treated entirely in terms of the geometry of a curved spacetime.
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In each of these spheres, every point can be carried to any other by an appropriate rotation about the centre of symmetry.

A photon sphere or photon circle arises in a neighbourhood of the event horizon of a black hole where gravity is so strong that emitted photons will not just bend around the black hole but also return to the point where they were emitted from and consequently display boomerang-like properties. As the source emitting photons falls into the gravitational field towards the event horizon the shape of the trajectory of each boomerang photon changes, tending to a more circular form. At a critical value of the radial distance from the singularity the trajectory of a boomerang photon will take the form of a non-stable circular orbit, thus forming a photon circle and hence in aggregation a photon sphere. The circular photon orbit is said to be the last photon orbit. The radius of the photon sphere, which is also the lower bound for any stable orbit, is, for a Schwarzschild black hole,
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".

In geometry, a spherical sector, also known as a spherical cone, is a portion of a sphere or of a ball defined by a conical boundary with apex at the center of the sphere. It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. It is the three-dimensional analogue of the sector of a circle.
In the theory of Lorentzian manifolds, spherically symmetric spacetimes admit a family of nested round spheres. In such a spacetime, a particularly important kind of coordinate chart is the Schwarzschild chart, a kind of polar spherical coordinate chart on a static and spherically symmetric spacetime, which is adapted to these nested round spheres. The defining characteristic of Schwarzschild chart is that the radial coordinate possesses a natural geometric interpretation in terms of the surface area and Gaussian curvature of each sphere. However, radial distances and angles are not accurately represented.
In general relativity, the Weyl metrics are a class of static and axisymmetric solutions to Einstein's field equation. Three members in the renowned Kerr–Newman family solutions, namely the Schwarzschild, nonextremal Reissner–Nordström and extremal Reissner–Nordström metrics, can be identified as Weyl-type metrics.
In Einstein's theory of general relativity, the interior Schwarzschild metric is an exact solution for the gravitational field in the interior of a non-rotating spherical body which consists of an incompressible fluid and has zero pressure at the surface. This is a static solution, meaning that it does not change over time. It was discovered by Karl Schwarzschild in 1916, who earlier had found the exterior Schwarzschild metric.




























