
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another. The field of navigation includes four general categories: land navigation, marine navigation, aeronautic navigation, and space navigation.

A sextant is a doubly reflecting navigation instrument that measures the angular distance between two visible objects. The primary use of a sextant is to measure the angle between an astronomical object and the horizon for the purposes of celestial navigation.
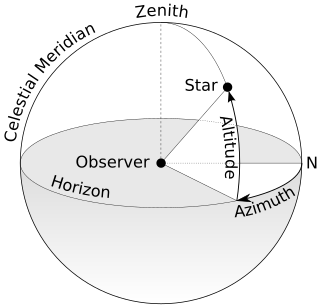
An azimuth is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.

Celestial navigation, also known as astronavigation, is the practice of position fixing using stars and other celestial bodies that enables a navigator to accurately determine their actual current physical position in space or on the surface of the Earth without relying solely on estimated positional calculations, commonly known as dead reckoning. Celestial navigation is performed without using satellite navigation or other similar modern electronic or digital positioning means.

In navigation, bearing or azimuth is the horizontal angle between the direction of an object and north or another object. The angle value can be specified in various angular units, such as degrees, mils, or grad. More specifically:
Navigational instruments are instruments used by nautical navigators and pilots as tools of their trade. The purpose of navigation is to ascertain the present position and to determine the speed, direction, etc. to arrive at the port or point of destination.

The term Jacob's staff is used to refer to several things, also known as cross-staff, a ballastella, a fore-staff, a ballestilla, or a balestilha. In its most basic form, a Jacob's staff is a stick or pole with length markings; most staffs are much more complicated than that, and usually contain a number of measurement and stabilization features. The two most frequent uses are:

The octant, also called a reflecting quadrant, is a reflecting instrument used in navigation.

Visual angle is the angle a viewed object subtends at the eye, usually stated in degrees of arc. It also is called the object's angular size.
In astronomical navigation, the intercept method, also known as Marcq St. Hilaire method, is a method of calculating an observer's position on Earth (geopositioning). It was originally called the azimuth intercept method because the process involves drawing a line which intercepts the azimuth line. This name was shortened to intercept method and the intercept distance was shortened to 'intercept'.

Longitude by chronometer is a method, in navigation, of determining longitude using a marine chronometer, which was developed by John Harrison during the first half of the eighteenth century. It is an astronomical method of calculating the longitude at which a position line, drawn from a sight by sextant of any celestial body, crosses the observer's assumed latitude. In order to calculate the position line, the time of the sight must be known so that the celestial position i.e. the Greenwich Hour Angle and Declination, of the observed celestial body is known. All that can be derived from a single sight is a single position line, which can be achieved at any time during daylight when both the sea horizon and the sun are visible. To achieve a fix, more than one celestial body and the sea horizon must be visible. This is usually only possible at dawn and dusk.
Ex-meridian is a celestial navigation method of calculating an observer's position on Earth. The method gives the observer a position line on which the observer is situated. It is usually used when the Sun is obscured at noon, and as a result, a meridian altitude is not possible. The navigator measures the altitude of the Sun as close to noon as possible and then calculates where the position line lies.
Meridian altitude is a method of celestial navigation to calculate an observer's latitude. It notes the altitude angle of an astronomical object above the horizon at culmination.

In celestial navigation, lunar distance, also called a lunar, is the angular distance between the Moon and another celestial body. The lunar distances method uses this angle and a nautical almanac to calculate Greenwich time if so desired, or by extension any other time. That calculated time can be used in solving a spherical triangle. The theory was first published by Johannes Werner in 1524, before the necessary almanacs had been published. A fuller method was published in 1763 and used until about 1850 when it was superseded by the marine chronometer. A similar method uses the positions of the Galilean moons of Jupiter.
The navigational triangle or PZX triangle is a spherical triangle used in astronavigation to determine the observer's position on the globe. It is composed of three reference points on the celestial sphere:
In astronomy, sextants are devices depicting a sixth of a circle, used primarily for measuring the position of stars. There are two types of astronomical sextants, mural instruments and frame-based instruments.

A quadrant is an instrument used to measure angles up to 90°. Different versions of this instrument could be used to calculate various readings, such as longitude, latitude, and time of day. Its earliest recorded usage was in ancient India in Rigvedic times by Rishi Atri to observe a solar eclipse. It was then proposed by Ptolemy as a better kind of astrolabe. Several different variations of the instrument were later produced by medieval Muslim astronomers. Mural quadrants were important astronomical instruments in 18th-century European observatories, establishing a use for positional astronomy.
Reflecting instruments are those that use mirrors to enhance their ability to make measurements. In particular, the use of mirrors permits one to observe two objects simultaneously while measuring the angular distance between the objects. While reflecting instruments are used in many professions, they are primarily associated with celestial navigation as the need to solve navigation problems, in particular the problem of the longitude, was the primary motivation in their development.

The circle of equal altitude, also called circle of position (CoP), is defined as the locus of points on Earth on which an observer sees a celestial object such as the sun or a star, at a given time, with the same observed altitude. It was discovered by the American sea-captain Thomas Hubbard Sumner in 1837, published in 1843 and is the basis of an important method in celestial navigation.
The Greeks studied the results of the measurements of latitude by the explorer Pytheas who voyaged to Britain and beyond, as far as the Arctic Circle, in 325 BC. They used several methods to measure latitude, including the height of the Sun above the horizon at midday, measured using a gnōmōn ; the length of the day at the summer solstice, and the elevation of the Sun at winter solstice.



















