
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.

A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.

In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic that gives conditions for the solvability of quadratic equations modulo prime numbers. Due to its subtlety, it has many formulations, but the most standard statement is:

In number theory, a Gaussian integer is a complex number whose real and imaginary parts are both integers. The Gaussian integers, with ordinary addition and multiplication of complex numbers, form an integral domain, usually written as or
In mathematics, a unique factorization domain (UFD) is a ring in which a statement analogous to the fundamental theorem of arithmetic holds. Specifically, a UFD is an integral domain in which every non-zero non-unit element can be written as a product of prime elements, uniquely up to order and units.
In number theory, a prime number p is a Sophie Germain prime if 2p + 1 is also prime. The number 2p + 1 associated with a Sophie Germain prime is called a safe prime. For example, 11 is a Sophie Germain prime and 2 × 11 + 1 = 23 is its associated safe prime. Sophie Germain primes are named after French mathematician Sophie Germain, who used them in her investigations of Fermat's Last Theorem. One attempt by Germain to prove Fermat’s Last Theorem was to let p be a prime number of the form 8k + 7 and to let n = p – 1. In this case, is unsolvable. Germain’s proof, however, remained unfinished. Through her attempts to solve Fermat's Last Theorem, Germain developed a result now known as Germain's Theorem which states that if p is an odd prime and 2p + 1 is also prime, then p must divide x, y, or z. Otherwise, . This case where p does not divide x, y, or z is called the first case. Sophie Germain’s work was the most progress achieved on Fermat’s last theorem at that time. Later work by Kummer and others always divided the problem into first and second cases. Sophie Germain primes and safe primes have applications in public key cryptography and primality testing. It has been conjectured that there are infinitely many Sophie Germain primes, but this remains unproven.
In number theory, Euler's criterion is a formula for determining whether an integer is a quadratic residue modulo a prime. Precisely,
In number theory, an integer q is called a quadratic residue modulo n if it is congruent to a perfect square modulo n; i.e., if there exists an integer x such that:
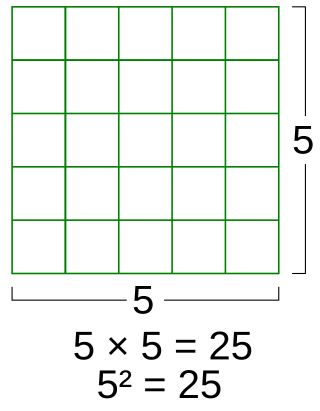
In mathematics, a square is the result of multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as raising to the power 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations x^2 (caret) or x**2 may be used in place of x2. The adjective which corresponds to squaring is quadratic.

In number theory, the nth Pisano period, written as π(n), is the period with which the sequence of Fibonacci numbers taken modulo n repeats. Pisano periods are named after Leonardo Pisano, better known as Fibonacci. The existence of periodic functions in Fibonacci numbers was noted by Joseph Louis Lagrange in 1774.
In additive number theory, Fermat's theorem on sums of two squares states that an odd prime p can be expressed as:
In mathematics, a binary quadratic form is a quadratic homogeneous polynomial in two variables
In number theory, Meyer's theorem on quadratic forms states that an indefinite quadratic form Q in five or more variables over the field of rational numbers nontrivially represents zero. In other words, if the equation
In mathematics, the sieve of Atkin is a modern algorithm for finding all prime numbers up to a specified integer. Compared with the ancient sieve of Eratosthenes, which marks off multiples of primes, the sieve of Atkin does some preliminary work and then marks off multiples of squares of primes, thus achieving a better theoretical asymptotic complexity. It was created in 2003 by A. O. L. Atkin and Daniel J. Bernstein.
The Erdős–Straus conjecture is an unproven statement in number theory. The conjecture is that, for every integer that is 2 or more, there exist positive integers , , and for which

A Pythagorean prime is a prime number of the form . Pythagorean primes are exactly the odd prime numbers that are the sum of two squares; this characterization is Fermat's theorem on sums of two squares.

Irving Kaplansky was a mathematician, college professor, author, and amateur musician.
In algebraic number theory, a fundamental unit is a generator for the unit group of the ring of integers of a number field, when that group has rank 1. Dirichlet's unit theorem shows that the unit group has rank 1 exactly when the number field is a real quadratic field, a complex cubic field, or a totally imaginary quartic field. When the unit group has rank ≥ 1, a basis of it modulo its torsion is called a fundamental system of units. Some authors use the term fundamental unit to mean any element of a fundamental system of units, not restricting to the case of rank 1.
In abstract algebra, a multiplicatively closed set is a subset S of a ring R such that the following two conditions hold:
In number theory, a cyclotomic field is a number field obtained by adjoining a complex root of unity to Q, the field of rational numbers.