
Bessel functions, first defined by the mathematician Daniel Bernoulli and then generalized by Friedrich Bessel, are canonical solutions y(x) of Bessel's differential equation
In integral calculus, an elliptic integral is one of a number of related functions defined as the value of certain integrals, which were first studied by Giulio Fagnano and Leonhard Euler. Their name originates from their originally arising in connection with the problem of finding the arc length of an ellipse.

The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as and . They can be defined in several equivalent ways, one of which starts with trigonometric functions:

In probability theory and statistics, the gamma distribution is a two-parameter family of continuous probability distributions. The exponential distribution, Erlang distribution, and chi-squared distribution are special cases of the gamma distribution. There are two equivalent parameterizations in common use:
- With a shape parameter and a scale parameter .
- With a shape parameter and an inverse scale parameter , called a rate parameter.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform. This integral transform is closely connected to the theory of Dirichlet series, and is often used in number theory, mathematical statistics, and the theory of asymptotic expansions; it is closely related to the Laplace transform and the Fourier transform, and the theory of the gamma function and allied special functions.
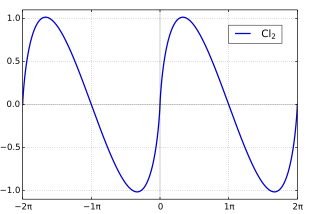
In mathematics, the Clausen function, introduced by Thomas Clausen (1832), is a transcendental, special function of a single variable. It can variously be expressed in the form of a definite integral, a trigonometric series, and various other forms. It is intimately connected with the polylogarithm, inverse tangent integral, polygamma function, Riemann zeta function, Dirichlet eta function, and Dirichlet beta function.

In mathematics, theta functions are special functions of several complex variables. They show up in many topics, including Abelian varieties, moduli spaces, quadratic forms, and solitons. As Grassmann algebras, they appear in quantum field theory.

In mathematics, physics and engineering, the sinc function, denoted by sinc(x), has two forms, normalized and unnormalized.
In mathematics, the Hankel transform expresses any given function f(r) as the weighted sum of an infinite number of Bessel functions of the first kind Jν(kr). The Bessel functions in the sum are all of the same order ν, but differ in a scaling factor k along the r axis. The necessary coefficient Fν of each Bessel function in the sum, as a function of the scaling factor k constitutes the transformed function. The Hankel transform is an integral transform and was first developed by the mathematician Hermann Hankel. It is also known as the Fourier–Bessel transform. Just as the Fourier transform for an infinite interval is related to the Fourier series over a finite interval, so the Hankel transform over an infinite interval is related to the Fourier–Bessel series over a finite interval.
In mathematics, in the area of complex analysis, Nachbin's theorem is commonly used to establish a bound on the growth rates for an analytic function. This article provides a brief review of growth rates, including the idea of a function of exponential type. Classification of growth rates based on type help provide a finer tool than big O or Landau notation, since a number of theorems about the analytic structure of the bounded function and its integral transforms can be stated. In particular, Nachbin's theorem may be used to give the domain of convergence of the generalized Borel transform, given below.
In mathematics, the Bessel polynomials are an orthogonal sequence of polynomials. There are a number of different but closely related definitions. The definition favored by mathematicians is given by the series
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). It was introduced in 1927 by Eugene Wigner, and plays a fundamental role in the quantum mechanical theory of angular momentum. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The letter D stands for Darstellung, which means "representation" in German.
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load.
In mathematics, a Jackson q-Bessel function is one of the three q-analogs of the Bessel function introduced by Jackson. The third Jackson q-Bessel function is the same as the Hahn–Exton q-Bessel function.
In fluid dynamics, Taylor scraping flow is a type of two-dimensional corner flow occurring when one of the wall is sliding over the other with constant velocity, named after G. I. Taylor.
Schlömilch's series is a Fourier series type expansion of twice continuously differentiable function in the interval in terms of the Bessel function of the first kind, named after the German mathematician Oskar Schlömilch, who derived the series in 1857. The real-valued function has the following expansion:

In probability theory, the stable count distribution is the conjugate prior of a one-sided stable distribution. This distribution was discovered by Stephen Lihn in his 2017 study of daily distributions of the S&P 500 and the VIX. The stable distribution family is also sometimes referred to as the Lévy alpha-stable distribution, after Paul Lévy, the first mathematician to have studied it.
































