
Ionization is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule is called an ion. Ionization can result from the loss of an electron after collisions with subatomic particles, collisions with other atoms, molecules, electrons, positrons, protons, antiprotons and ions, or through the interaction with electromagnetic radiation. Heterolytic bond cleavage and heterolytic substitution reactions can result in the formation of ion pairs. Ionization can occur through radioactive decay by the internal conversion process, in which an excited nucleus transfers its energy to one of the inner-shell electrons causing it to be ejected.
In quantum chemistry and molecular physics, the Born–Oppenheimer (BO) approximation is the best-known mathematical approximation in molecular dynamics. Specifically, it is the assumption that the wave functions of atomic nuclei and electrons in a molecule can be treated separately, based on the fact that the nuclei are much heavier than the electrons. Due to the larger relative mass of a nucleus compared to an electron, the coordinates of the nuclei in a system are approximated as fixed, while the coordinates of the electrons are dynamic. The approach is named after Max Born and his 23-year-old graduate student J. Robert Oppenheimer, the latter of whom proposed it in 1927 during a period of intense fervent in the development of quantum mechanics.
Density functional theory (DFT) is a computational quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. Using this theory, the properties of a many-electron system can be determined by using functionals, i.e. functions of another function. In the case of DFT, these are functionals of the spatially dependent electron density. DFT is among the most popular and versatile methods available in condensed-matter physics, computational physics, and computational chemistry.
Electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial variables and is typically denoted as either or . The density is determined, through definition, by the normalised -electron wavefunction which itself depends upon variables. Conversely, the density determines the wave function modulo up to a phase factor, providing the formal foundation of density functional theory.
Slater-type orbitals (STOs) are functions used as atomic orbitals in the linear combination of atomic orbitals molecular orbital method. They are named after the physicist John C. Slater, who introduced them in 1930.
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state.
In quantum mechanics, a Slater determinant is an expression that describes the wave function of a multi-fermionic system. It satisfies anti-symmetry requirements, and consequently the Pauli principle, by changing sign upon exchange of two electrons. Only a small subset of all possible fermionic wave functions can be written as a single Slater determinant, but those form an important and useful subset because of their simplicity.
Jellium, also known as the uniform electron gas (UEG) or homogeneous electron gas (HEG), is a quantum mechanical model of interacting electrons in a solid where the positive charges are assumed to be uniformly distributed in space; the electron density is a uniform quantity as well in space. This model allows one to focus on the effects in solids that occur due to the quantum nature of electrons and their mutual repulsive interactions without explicit introduction of the atomic lattice and structure making up a real material. Jellium is often used in solid-state physics as a simple model of delocalized electrons in a metal, where it can qualitatively reproduce features of real metals such as screening, plasmons, Wigner crystallization and Friedel oscillations.
In quantum mechanics, the Hellmann–Feynman theorem relates the derivative of the total energy with respect to a parameter to the expectation value of the derivative of the Hamiltonian with respect to that same parameter. According to the theorem, once the spatial distribution of the electrons has been determined by solving the Schrödinger equation, all the forces in the system can be calculated using classical electrostatics.
Time-dependent density-functional theory (TDDFT) is a quantum mechanical theory used in physics and chemistry to investigate the properties and dynamics of many-body systems in the presence of time-dependent potentials, such as electric or magnetic fields. The effect of such fields on molecules and solids can be studied with TDDFT to extract features like excitation energies, frequency-dependent response properties, and photoabsorption spectra.
The Kohn-Sham equations are a set of mathematical equations used in quantum mechanics to simplify the complex problem of understanding how electrons behave in atoms and molecules. They introduce fictitious non-interacting electrons and use them to find the most stable arrangement of electrons, which helps scientists understand and predict the properties of matter at the atomic and molecular scale.
In atomic, molecular, and optical physics and quantum chemistry, the molecular Hamiltonian is the Hamiltonian operator representing the energy of the electrons and nuclei in a molecule. This operator and the associated Schrödinger equation play a central role in computational chemistry and physics for computing properties of molecules and aggregates of molecules, such as thermal conductivity, specific heat, electrical conductivity, optical, and magnetic properties, and reactivity.
In condensed matter physics, the independent electron approximation is a simplification used in complex systems, consisting of many electrons, that approximates the electron–electron interaction in crystals as null. It is a requirement for both the free electron model and the nearly-free electron model, where it is used alongside Bloch's theorem. In quantum mechanics, this approximation is often used to simplify a quantum many-body problem into single-particle approximations.
Hooke's atom, also known as harmonium or hookium, refers to an artificial helium-like atom where the Coulombic electron-nucleus interaction potential is replaced by a harmonic potential. This system is of significance as it is, for certain values of the force constant defining the harmonic containment, an exactly solvable ground-state many-electron problem that explicitly includes electron correlation. As such it can provide insight into quantum correlation and can act as a test system for judging the accuracy of approximate quantum chemical methods for solving the Schrödinger equation. The name "Hooke's atom" arises because the harmonic potential used to describe the electron-nucleus interaction is a consequence of Hooke's law.
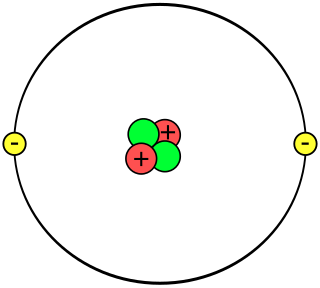
A helium atom is an atom of the chemical element helium. Helium is composed of two electrons bound by the electromagnetic force to a nucleus containing two protons along with two neutrons, depending on the isotope, held together by the strong force. Unlike for hydrogen, a closed-form solution to the Schrödinger equation for the helium atom has not been found. However, various approximations, such as the Hartree–Fock method, can be used to estimate the ground state energy and wavefunction of the atom. Historically, the first such helium spectrum calculation was done by Albrecht Unsöld in 1927. Its success was considered to be one of the earliest signs of validity of Schrödinger's wave mechanics.
The Holstein–Herring method, also called the surface integral method, or Smirnov's method is an effective means of getting the exchange energy splittings of asymptotically degenerate energy states in molecular systems. Although the exchange energy becomes elusive at large internuclear systems, it is of prominent importance in theories of molecular binding and magnetism. This splitting results from the symmetry under exchange of identical nuclei. The basic idea pioneered by Theodore Holstein, Conyers Herring and Boris M. Smirnov in the 1950-1960.
The quantum rotor model is a mathematical model for a quantum system. It can be visualized as an array of rotating electrons which behave as rigid rotors that interact through short-range dipole-dipole magnetic forces originating from their magnetic dipole moments. The model differs from similar spin-models such as the Ising model and the Heisenberg model in that it includes a term analogous to kinetic energy.
In quantum mechanics, orbital magnetization, Morb, refers to the magnetization induced by orbital motion of charged particles, usually electrons in solids. The term "orbital" distinguishes it from the contribution of spin degrees of freedom, Mspin, to the total magnetization. A nonzero orbital magnetization requires broken time-reversal symmetry, which can occur spontaneously in ferromagnetic and ferrimagnetic materials, or can be induced in a non-magnetic material by an applied magnetic field.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is thermal energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.

In quantum optics, a superradiant phase transition is a phase transition that occurs in a collection of fluorescent emitters, between a state containing few electromagnetic excitations and a superradiant state with many electromagnetic excitations trapped inside the emitters. The superradiant state is made thermodynamically favorable by having strong, coherent interactions between the emitters.






