
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties. This is often written as or where is the Laplace operator, is the divergence operator, is the gradient operator, and is a twice-differentiable real-valued function. The Laplace operator therefore maps a scalar function to another scalar function.

An ellipsoid is a surface that can be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
In physics, the CHSH inequality can be used in the proof of Bell's theorem, which states that certain consequences of entanglement in quantum mechanics cannot be reproduced by local hidden-variable theories. Experimental verification of the inequality being violated is seen as confirmation that nature cannot be described by such theories. CHSH stands for John Clauser, Michael Horne, Abner Shimony, and Richard Holt, who described it in a much-cited paper published in 1969. They derived the CHSH inequality, which, as with John Stewart Bell's original inequality, is a constraint—on the statistical occurrence of "coincidences" in a Bell test—which is necessarily true if an underlying local hidden-variable theory exists. In practice, the inequality is routinely violated by modern experiments in quantum mechanics.

In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields. The table of spherical harmonics contains a list of common spherical harmonics.
Fourier optics is the study of classical optics using Fourier transforms (FTs), in which the waveform being considered is regarded as made up of a combination, or superposition, of plane waves. It has some parallels to the Huygens–Fresnel principle, in which the wavefront is regarded as being made up of a combination of spherical wavefronts whose sum is the wavefront being studied. A key difference is that Fourier optics considers the plane waves to be natural modes of the propagation medium, as opposed to Huygens–Fresnel, where the spherical waves originate in the physical medium.
In probability theory, the Borel–Kolmogorov paradox is a paradox relating to conditional probability with respect to an event of probability zero. It is named after Émile Borel and Andrey Kolmogorov.
In mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation
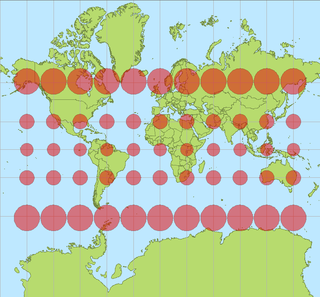
In cartography, a Tissot's indicatrix is a mathematical contrivance presented by French mathematician Nicolas Auguste Tissot in 1859 and 1871 in order to characterize local distortions due to map projection. It is the geometry that results from projecting a circle of infinitesimal radius from a curved geometric model, such as a globe, onto a map. Tissot proved that the resulting diagram is an ellipse whose axes indicate the two principal directions along which scale is maximal and minimal at that point on the map.

In electromagnetics, directivity is a parameter of an antenna or optical system which measures the degree to which the radiation emitted is concentrated in a single direction. It is the ratio of the radiation intensity in a given direction from the antenna to the radiation intensity averaged over all directions. Therefore, the directivity of a hypothetical isotropic radiator is 1, or 0 dBi.
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as . Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential.
In special functions, a topic in mathematics, spin-weighted spherical harmonics are generalizations of the standard spherical harmonics and—like the usual spherical harmonics—are functions on the sphere. Unlike ordinary spherical harmonics, the spin-weighted harmonics are U(1) gauge fields rather than scalar fields: mathematically, they take values in a complex line bundle. The spin-weighted harmonics are organized by degree l, just like ordinary spherical harmonics, but have an additional spin weights that reflects the additional U(1) symmetry. A special basis of harmonics can be derived from the Laplace spherical harmonics Ylm, and are typically denoted by sYlm, where l and m are the usual parameters familiar from the standard Laplace spherical harmonics. In this special basis, the spin-weighted spherical harmonics appear as actual functions, because the choice of a polar axis fixes the U(1) gauge ambiguity. The spin-weighted spherical harmonics can be obtained from the standard spherical harmonics by application of spin raising and lowering operators. In particular, the spin-weighted spherical harmonics of spin weight s = 0 are simply the standard spherical harmonics:
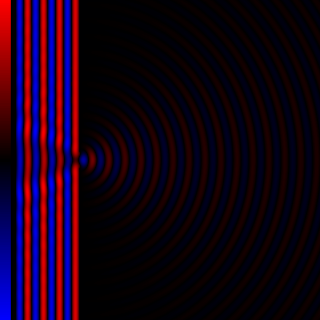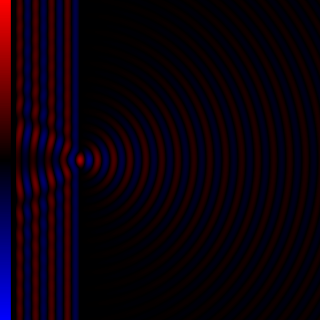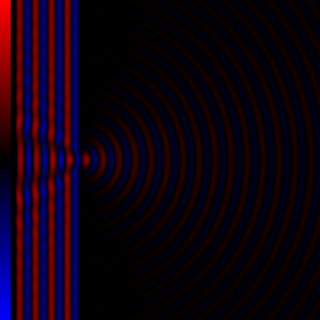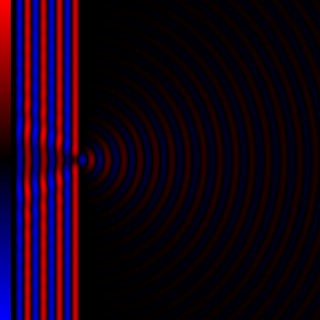
Diffraction processes affecting waves are amenable to quantitative description and analysis. Such treatments are applied to a wave passing through one or more slits whose width is specified as a proportion of the wavelength. Numerical approximations may be used, including the Fresnel and Fraunhofer approximations.
In mathematics, vector spherical harmonics (VSH) are an extension of the scalar spherical harmonics for use with vector fields. The components of the VSH are complex-valued functions expressed in the spherical coordinate basis vectors.
In mathematics, the spectral theory of ordinary differential equations is the part of spectral theory concerned with the determination of the spectrum and eigenfunction expansion associated with a linear ordinary differential equation. In his dissertation, Hermann Weyl generalized the classical Sturm–Liouville theory on a finite closed interval to second order differential operators with singularities at the endpoints of the interval, possibly semi-infinite or infinite. Unlike the classical case, the spectrum may no longer consist of just a countable set of eigenvalues, but may also contain a continuous part. In this case the eigenfunction expansion involves an integral over the continuous part with respect to a spectral measure, given by the Titchmarsh–Kodaira formula. The theory was put in its final simplified form for singular differential equations of even degree by Kodaira and others, using von Neumann's spectral theorem. It has had important applications in quantum mechanics, operator theory and harmonic analysis on semisimple Lie groups.

In general relativity, a point mass deflects a light ray with impact parameter by an angle approximately equal to
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.

Geographical distance or geodetic distance is the distance measured along the surface of the Earth, or the shortest arch length.

The first description of multiple-prism arrays, and multiple-prism dispersion, was given by Newton in his book Opticks. Prism pair expanders were introduced by Brewster in 1813. A modern mathematical description of the single-prism dispersion was given by Born and Wolf in 1959. The generalized multiple-prism dispersion theory was introduced by Duarte and Piper in 1982.
In general relativity, the Vaidya metric describes the non-empty external spacetime of a spherically symmetric and nonrotating star which is either emitting or absorbing null dusts. It is named after the Indian physicist Prahalad Chunnilal Vaidya and constitutes the simplest non-static generalization of the non-radiative Schwarzschild solution to Einstein's field equation, and therefore is also called the "radiating(shining) Schwarzschild metric".
Chandrasekhar–Page equations describe the wave function of the spin-1/2 massive particles, that resulted by seeking a separable solution to the Dirac equation in Kerr metric or Kerr–Newman metric. In 1976, Subrahmanyan Chandrasekhar showed that a separable solution can be obtained from the Dirac equation in Kerr metric. Later, Don Page extended this work to Kerr–Newman metric, that is applicable to charged black holes. In his paper, Page notices that N. Toop also derived his results independently, as informed to him by Chandrasekhar.



























