
In computer science, a heap is a tree-based data structure that satisfies the heap property: In a max heap, for any given node C, if P is a parent node of C, then the key of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap is called the root node.
In computer science, a priority queue is an abstract data-type similar to a regular queue or stack data structure. Each element in a priority queue has an associated priority. In a priority queue, elements with high priority are served before elements with low priority. In some implementations, if two elements have the same priority, they are served in the same order in which they were enqueued. In other implementations, the order of elements with the same priority is undefined.

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues. The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.
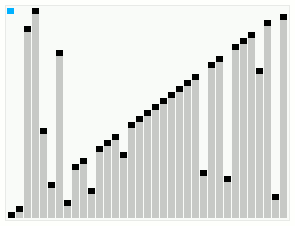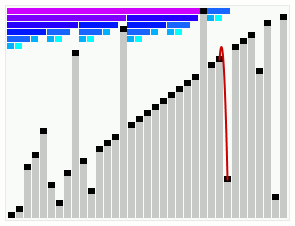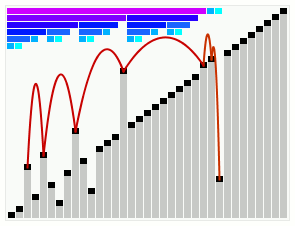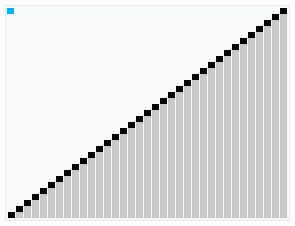
In computer science, smoothsort is a comparison-based sorting algorithm. A variant of heapsort, it was invented and published by Edsger Dijkstra in 1981. Like heapsort, smoothsort is an in-place algorithm with an upper bound of O(n log n) operations (see big O notation), but it is not a stable sort. The advantage of smoothsort is that it comes closer to O(n) time if the input is already sorted to some degree, whereas heapsort averages O(n log n) regardless of the initial sorted state.

In computer science, the treap and the randomized binary search tree are two closely related forms of binary search tree data structures that maintain a dynamic set of ordered keys and allow binary searches among the keys. After any sequence of insertions and deletions of keys, the shape of the tree is a random variable with the same probability distribution as a random binary tree; in particular, with high probability its height is proportional to the logarithm of the number of keys, so that each search, insertion, or deletion operation takes logarithmic time to perform.
In computer science, a binomial heap is a data structure that acts as a priority queue. It is an example of a mergeable heap, as it supports merging two heaps in logarithmic time. It is implemented as a heap similar to a binary heap but using a special tree structure that is different from the complete binary trees used by binary heaps. Binomial heaps were invented in 1978 by Jean Vuillemin.
In computer science, a Fibonacci heap is a data structure for priority queue operations. It has a better amortized running time than many other priority queue data structures including the binary heap and binomial heap. consisting of a collection of heap-ordered trees. Fibonacci heaps were originally explained to be an extension of binomial heaps. Michael L. Fredman and Robert E. Tarjan developed Fibonacci heaps in 1984 and published them in a scientific journal in 1987. Fibonacci heaps are named after the Fibonacci numbers, which are used in their running time analysis.

In computer science, a self-balancing binary search tree (BST) is any node-based binary search tree that automatically keeps its height small in the face of arbitrary item insertions and deletions. These operations when designed for a self-balancing binary search tree, contain precautionary measures against boundlessly increasing tree height, so that these abstract data structures receive the attribute "self-balancing".
In computer science, a leftist tree or leftist heap is a priority queue implemented with a variant of a binary heap. Every node x has an s-value which is the distance to the nearest leaf in subtree rooted at x. In contrast to a binary heap, a leftist tree attempts to be very unbalanced. In addition to the heap property, leftist trees are maintained so the right descendant of each node has the lower s-value.
A pairing heap is a type of heap data structure with relatively simple implementation and excellent practical amortized performance, introduced by Michael Fredman, Robert Sedgewick, Daniel Sleator, and Robert Tarjan in 1986. Pairing heaps are heap-ordered multiway tree structures, and can be considered simplified Fibonacci heaps. They are considered a "robust choice" for implementing such algorithms as Prim's MST algorithm, and support the following operations :
The d-ary heap or d-heap is a priority queue data structure, a generalization of the binary heap in which the nodes have d children instead of 2. Thus, a binary heap is a 2-heap, and a ternary heap is a 3-heap. According to Tarjan and Jensen et al., d-ary heaps were invented by Donald B. Johnson in 1975.

In computer science, a Cartesian tree is a binary tree derived from a sequence of distinct numbers. To construct the Cartesian tree, set its root to be the minimum number in the sequence, and recursively construct its left and right subtrees from the subsequences before and after this number. It is uniquely defined as a min-heap whose symmetric (in-order) traversal returns the original sequence.
In computer science, a min-max heap is a complete binary tree data structure which combines the usefulness of both a min-heap and a max-heap, that is, it provides constant time retrieval and logarithmic time removal of both the minimum and maximum elements in it. This makes the min-max heap a very useful data structure to implement a double-ended priority queue. Like binary min-heaps and max-heaps, min-max heaps support logarithmic insertion and deletion and can be built in linear time. Min-max heaps are often represented implicitly in an array; hence it's referred to as an implicit data structure.

A Kinetic Heap is a kinetic data structure, obtained by the kinetization of a heap. It is designed to store elements where the priority is changing as a continuous function of time. As a type of kinetic priority queue, it maintains the maximum priority element stored in it. The kinetic heap data structure works by storing the elements as a tree that satisfies the following heap property – if B is a child node of A, then the priority of the element in A must be higher than the priority of the element in B. This heap property is enforced using certificates along every edge so, like other kinetic data structures, a kinetic heap also contains a priority queue to maintain certificate failure times.
A kinetic closest pair data structure is a kinetic data structure that maintains the closest pair of points, given a set P of n points that are moving continuously with time in a metric space. While many efficient algorithms were known in the static case, they proved hard to kinetize, so new static algorithms were developed to solve this problem.

A Kinetic Tournament is a kinetic data structure that functions as a priority queue for elements whose priorities change as a continuous function of time. It is implemented analogously to a "tournament" between elements to determine the "winner", with the certificates enforcing the winner of each "match" in the tournament. It supports the usual priority queue operations - insert, delete and find-max. They are often used as components of other kinetic data structures, such as kinetic closest pair.
A Kinetic hanger is a randomized version of a kinetic heap whose performance is easy to analyze tightly. A kinetic hanger satisfies the heap property but relaxes the requirement that the tree structure must be strictly balanced, thus insertions and deletions can be randomized. As a result, the structure of the kinetic hanger has the property that it is drawn uniformly at random from the space of all possible heap-like structures on its elements.
A Kinetic Priority Queue is an abstract kinetic data structure. It is a variant of a priority queue designed to maintain the maximum priority element when the priority of every element is changing as a continuous function of time. Kinetic priority queues have been used as components of several kinetic data structures, as well as to solve some important non-kinetic problems such as the k-set problem and the connected red blue segments intersection problem.








