In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic at all finite points over the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any finite sums, products and compositions of these, such as the trigonometric functions sine and cosine and their hyperbolic counterparts sinh and cosh, as well as derivatives and integrals of entire functions such as the error function. If an entire function f(z) has a root at w, then f(z)/(z−w), taking the limit value at w, is an entire function. On the other hand, neither the natural logarithm nor the square root is an entire function, nor can they be continued analytically to an entire function.
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, mathematical analysis. Series are used in most areas of mathematics, even for studying finite structures, through generating functions. In addition to their ubiquity in mathematics, infinite series are also widely used in other quantitative disciplines such as physics, computer science, statistics and finance.

In probability theory, the normaldistribution is a very common continuous probability distribution. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. A random variable with a Gaussian distribution is said to be normally distributed and is called a normal deviate.
In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution even if the original variables themselves are not normally distributed. The theorem is a key concept in probability theory because it implies that probabilistic and statistical methods that work for normal distributions can be applicable to many problems involving other types of distributions.
In mathematics, a formal power series is a generalization of a polynomial, where the number of terms is allowed to be infinite; this implies giving up the possibility of replacing the variable in the polynomial with an arbitrary number. Thus a formal power series differs from a polynomial in that it may have infinitely many terms, and differs from a power series, whose variables can take on numerical values. One way to view a formal power series is as an infinite ordered sequence of numbers. In this case, the powers of the variable are used only to indicate the order of the coefficients, so that the coefficient of is the fifth term in the sequence. In combinatorics, formal power series provide representations of numerical sequences and of multisets, and for instance allow concise expressions for recursively defined sequences regardless of whether the recursion can be explicitly solved; this is known as the method of generating functions. More generally, formal power series can include series with any finite number of variables, and with coefficients in an arbitrary ring. Formal power series can be created from Taylor polynomials using formal moduli.
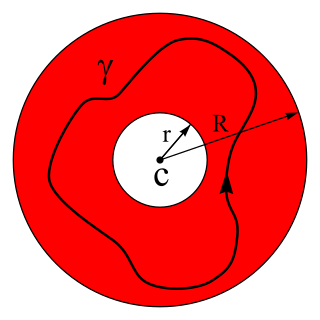
In mathematics, the Laurent series of a complex function f(z) is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass may have discovered it first in a paper written in 1841, but it was not published until after his death.
In mathematics, an infinite series of numbers is said to converge absolutely if the sum of the absolute values of the summands is finite. More precisely, a real or complex series is said to converge absolutely if for some real number . Similarly, an improper integral of a function, , is said to converge absolutely if the integral of the absolute value of the integrand is finite—that is, if
In the mathematical field of real analysis, the monotone convergence theorem is any of a number of related theorems proving the convergence of monotonic sequences that are also bounded. Informally, the theorems state that if a sequence is increasing and bounded above by a supremum, then the sequence will converge to the supremum; in the same way, if a sequence is decreasing and is bounded below by an infimum, it will converge to the infimum.
In mathematics, a Gaussian function, often simply referred to as a Gaussian, is a function of the form:
In mathematics, a Dirichlet series is any series of the form
In statistics, propagation of uncertainty is the effect of variables' uncertainties on the uncertainty of a function based on them. When the variables are the values of experimental measurements they have uncertainties due to measurement limitations which propagate due to the combination of variables in the function.
The Gram–Charlier A series, and the Edgeworth series are series that approximate a probability distribution in terms of its cumulants. The series are the same; but, the arrangement of terms differ. The key idea of these expansions is to write the characteristic function of the distribution whose probability density function f is to be approximated in terms of the characteristic function of a distribution with known and suitable properties, and to recover f through the inverse Fourier transform.
In mathematics, subadditivity is a property of a function that states, roughly, that evaluating the function for the sum of two elements of the domain always returns something less than or equal to the sum of the function's values at each element. There are numerous examples of subadditive functions in various areas of mathematics, particularly norms and square roots. Additive maps are special cases of subadditive functions.
In Bayesian statistics, a maximum a posteriori probability (MAP) estimate is an estimate of an unknown quantity, that equals the mode of the posterior distribution. The MAP can be used to obtain a point estimate of an unobserved quantity on the basis of empirical data. It is closely related to the method of maximum likelihood (ML) estimation, but employs an augmented optimization objective which incorporates a prior distribution over the quantity one wants to estimate. MAP estimation can therefore be seen as a regularization of ML estimation.

In probability theory, the Rice distribution, Rician distribution or Ricean distribution is the probability distribution of the magnitude of a circular bivariate normal random variable with potentially non-zero mean. It was named after Stephen O. Rice.
In statistical signal processing, the goal of spectral density estimation (SDE) is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal. One purpose of estimating the spectral density is to detect any periodicities in the data, by observing peaks at the frequencies corresponding to these periodicities.
In mathematics, and more specifically in numerical analysis, Householder's methods are a class of root-finding algorithms that are used for functions of one real variable with continuous derivatives up to some order d + 1. Each of these methods is characterized by the number d, which is known as the order of the method. The algorithm is iterative and has a rate of convergence of d + 1.

In numerical analysis, Gauss–Hermite quadrature is a form of Gaussian quadrature for approximating the value of integrals of the following kind:
In the field of mathematical analysis, a general Dirichlet series is an infinite series that takes the form of
In mathematics, Topological Recursion is a recursive definition of invariants of spectral curves. It has applications in enumerative geometry, random matrix theory, mathematical physics, string theory, knot theory.




















