Landau–Kolmogorov inequality

Last updated April 16, 2019

In mathematics, the Landau–Kolmogorov inequality, named after Edmund Landau and Andrey Kolmogorov, is the following family of interpolation inequalities between different derivatives of a function f defined on a subset T of the real numbers:^[1]

Mathematics Field of study concerning quantity, patterns and change

Mathematics includes the study of such topics as quantity, structure, space, and change.

Edmund Georg Hermann Landau was a German mathematician who worked in the fields of number theory and complex analysis.

Andrey Nikolaevich Kolmogorov was a Soviet mathematician who made significant contributions to the mathematics of probability theory, topology, intuitionistic logic, turbulence, classical mechanics, algorithmic information theory and computational complexity.

On the real line

For k = 1, n = 2, T=R the inequality was first proved by Edmund Landau^[2] with the sharp constant C(2, 1, R) = 2. Following contributions by Jacques Hadamard and Georgiy Shilov, Andrey Kolmogorov found the sharp constants and arbitrary n, k:^[3]

Jacques Salomon Hadamard ForMemRS was a French mathematician who made major contributions in number theory, complex function theory, differential geometry and partial differential equations.

Georgi Evgen'evich Shilov was a Soviet mathematician and expert in the field of functional analysis, who contributed to the theory of normed rings and generalized functions.

C(n,k,\mathbb {R} )=a_{n-k}a_{n}^{-1+k/n}~,

where a_n are the Favard constants.

On the half-line

Following work by Matorin and others, the extremising functions were found by Isaac Jacob Schoenberg,^[4] explicit forms for the sharp constants are however still unknown.

Isaac Jacob Schoenberg American mathematician

Isaac Jacob Schoenberg was a Romanian-American mathematician, known for his discovery of splines.

Generalisations

There are many generalisations, which are of the form

\|f^{(k)}\|_{L_{q}(T)}\leq K\cdot {\|f\|_{L_{p}(T)}^{\alpha }}\cdot {\|f^{(n)}\|_{L_{r}(T)}^{1-\alpha }}{\text{ for }}1\leq k<n.

Here all three norms can be different from each other (from L₁ to L_∞, with p=q=r=∞ in the classical case) and T may be the real axis, semiaxis or a closed segment.

The Kallman–Rota inequality generalizes the Landau–Kolmogorov inequalities from the derivative operator to more general contractions on Banach spaces.^[5]

In mathematics, the Kallman–Rota inequality, introduced by Kallman & Rota (1970), is a generalization of the Landau–Kolmogorov inequality to Banach spaces. It states that if A is the infinitesimal generator of a one-parameter contraction semigroup then

In operator theory, a discipline within mathematics, a bounded operator T: X → Y between normed vector spaces X and Y is said to be a contraction if its operator norm ||T|| ≤ 1. Every bounded operator becomes a contraction after suitable scaling. The analysis of contractions provides insight into the structure of operators, or a family of operators. The theory of contractions on Hilbert space is largely due to Béla Szőkefalvi-Nagy and Ciprian Foias.

In mathematics, more specifically in functional analysis, a Banach space is a complete normed vector space. Thus, a Banach space is a vector space with a metric that allows the computation of vector length and distance between vectors and is complete in the sense that a Cauchy sequence of vectors always converges to a well defined limit that is within the space.

Notes

↑ Weisstein, E.W. "Landau-Kolmogorov Constants". MathWorld--A Wolfram Web Resource.
↑ Landau, E. (1913). "Ungleichungen für zweimal differenzierbare Funktionen". Proc. London Math. Soc. 13: 43–49. doi:10.1112/plms/s2-13.1.43.
↑ Kolmogorov, A. (1949). "On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Interval". Amer. Math. Soc. Transl. 1–2: 233–243.
↑ Schoenberg, I.J. (1973). "The Elementary Case of Landau's Problem of Inequalities Between Derivatives". Amer. Math. Monthly. 80: 121–158. doi:10.2307/2318373.
↑ Kallman, Robert R.; Rota, Gian-Carlo (1970), "On the inequality $\Vert f^{\prime }\Vert ^{2}\leqq 4\Vert f\Vert \cdot \Vert f''\Vert$ ", Inequalities, II (Proc. Second Sympos., U.S. Air Force Acad., Colo., 1967), New York: Academic Press, pp. 187–192, MR 0278059 .

→

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Related Research Articles

In mathematics convolution is a mathematical operation on two functions to produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and to the process of computing it. Some features of convolution are similar to cross-correlation: for real-valued functions, of a continuous or discrete variable, it differs from cross-correlation only in that either $f (x)$ or $g (x)$ is reflected about the y-axis; thus it is a cross-correlation of $f (x)$ and $g (- x)$ , or $f (- x)$ and $g (x)$ . For continuous functions, the cross-correlation operator is the adjoint of the convolution operator.

In number theory, a Liouville number is a real number x with the property that, for every positive integer n, there exist integers p and q with q > 1 and such that

The Liouville function, denoted by λ(n) and named after Joseph Liouville, is an important function in number theory.

In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of $L p$ spaces.

In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant. It is named after the Russian mathematician Andrey Markov, although it appeared earlier in the work of Pafnuty Chebyshev, and many sources, especially in analysis, refer to it as Chebyshev's inequality or Bienaymé's inequality.

In mathematical analysis, a function of bounded variation, also known as $BV$ function, is a real-valued function whose total variation is bounded (finite): the graph of a function having this property is well behaved in a precise sense. For a continuous function of a single variable, being of bounded variation means that the distance along the direction of the $y$ -axis, neglecting the contribution of motion along $x$ -axis, traveled by a point moving along the graph has a finite value. For a continuous function of several variables, the meaning of the definition is the same, except for the fact that the continuous path to be considered cannot be the whole graph of the given function, but can be every intersection of the graph itself with a hyperplane parallel to a fixed $x$ -axis and to the $y$ -axis.

In linear algebra, functional analysis, and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to each vector in a vector space—except for the zero vector, which is assigned a length of zero. A seminorm, on the other hand, is allowed to assign zero length to some non-zero vectors.

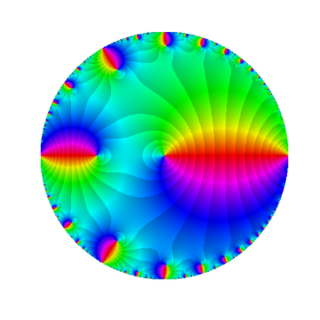
In mathematics, a Lambert series, named for Johann Heinrich Lambert, is a series taking the form

In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.

In mathematics, weak convergence in a Hilbert space is convergence of a sequence of points in the weak topology.

In mathematics, the Kolmogorov continuity theorem is a theorem that guarantees that a stochastic process that satisfies certain constraints on the moments of its increments will be continuous. It is credited to the Soviet mathematician Andrey Nikolaevich Kolmogorov.

In mathematical analysis, the Schur test, named after German mathematician Issai Schur, is a bound on the $operator norm of an integral operator in terms of its Schwartz kernel.$

In mathematics, in the field of functional analysis, the Cotlar–Stein almost orthogonality lemma is named after mathematicians Mischa Cotlar and Elias Stein. It may be used to obtain information on the operator norm on an operator, acting from one Hilbert space into another when the operator can be decomposed into almost orthogonal pieces. The original version of this lemma (for self-adjoint and mutually commuting operators) was proved by Mischa Cotlar in 1955 and allowed him to conclude that the Hilbert transform is a continuous linear operator in $without using the Fourier transform. A more general version was proved by Elias Stein.$

In functional analysis, the dual norm is a measure of the "size" of each continuous linear functional defined on a normed vector space.

In mathematics, particularly numerical analysis, the Bramble–Hilbert lemma, named after James H. Bramble and Stephen Hilbert, bounds the error of an approximation of a function $by a polynomial of order at most in terms of derivatives of of order . Both the error of the approximation and the derivatives of are measured by norms on a bounded domain in . This is similar to classical numerical analysis, where, for example, the error of linear interpolation can be bounded using the second derivative of . However, the Bramble-Hilbert lemma applies in any number of dimensions, not just one dimension, and the approximation error and the derivatives of are measured by more general norms involving averages, not just the maximum norm.$

In mathematics, the class of Muckenhoupt weights $A p$ consists of those weights $ω$ for which the Hardy–Littlewood maximal operator is bounded on $L p (dω)$ . Specifically, we consider functions $f$ on $R n$ and their associated maximal functions $M (f)$ defined as

In mathematical analysis, Lorentz spaces, introduced by George Lorentz in the 1950s, are generalisations of the more familiar $spaces$ .

Rodion Osievich Kuzmin was a Russian mathematician, known for his works in number theory and analysis. His name is sometimes transliterated as Kusmin. He was an Invited Speaker of the ICM in 1928 in Bologna.

In statistical learning theory, a representer theorem is any of several related results stating that a minimizer $of a regularized empirical risk function defined over a reproducing kernel Hilbert space can be represented as a finite linear combination of kernel products evaluated on the input points in the training set data.$

[1] Weisstein, E.W. "Landau-Kolmogorov Constants". MathWorld--A Wolfram Web Resource.

[2] Landau, E. (1913). "Ungleichungen für zweimal differenzierbare Funktionen". Proc. London Math. Soc. 13: 43–49. doi:10.1112/plms/s2-13.1.43.

[3] Kolmogorov, A. (1949). "On Inequalities Between the Upper Bounds of the Successive Derivatives of an Arbitrary Function on an Infinite Interval". Amer. Math. Soc. Transl. 1–2: 233–243.

[4] Schoenberg, I.J. (1973). "The Elementary Case of Landau's Problem of Inequalities Between Derivatives". Amer. Math. Monthly. 80: 121–158. doi:10.2307/2318373.

[5] Kallman, Robert R.; Rota, Gian-Carlo (1970), "On the inequality $\Vert f^{\prime }\Vert ^{2}\leqq 4\Vert f\Vert \cdot \Vert f''\Vert$ ", Inequalities, II (Proc. Second Sympos., U.S. Air Force Acad., Colo., 1967), New York: Academic Press, pp. 187–192, MR 0278059 .