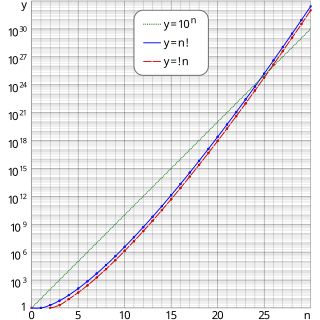
In mathematics, the factorial of a non-negative integer , denoted by , is the product of all positive integers less than or equal to . The factorial of also equals the product of with the next smaller factorial: For example, The value of 0! is 1, according to the convention for an empty product.
In combinatorial mathematics, a derangement is a permutation of the elements of a set in which no element appears in its original position. In other words, a derangement is a permutation that has no fixed points.
In combinatorial mathematics, the Bell numbers count the possible partitions of a set. These numbers have been studied by mathematicians since the 19th century, and their roots go back to medieval Japan. In an example of Stigler's law of eponymy, they are named after Eric Temple Bell, who wrote about them in the 1930s.

Ronald Lewis Graham was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.

In mathematics, the double factorial of a number n, denoted by n‼, is the product of all the positive integers up to n that have the same parity as n. That is,
In mathematics, a combinatorial class is a countable set of mathematical objects, together with a size function mapping each object to a non-negative integer, such that there are finitely many objects of each size.

In combinatorial mathematics, a de Bruijn sequence of order n on a size-k alphabet A is a cyclic sequence in which every possible length-n string on A occurs exactly once as a substring (i.e., as a contiguous subsequence). Such a sequence is denoted by B(k, n) and has length kn, which is also the number of distinct strings of length n on A. Each of these distinct strings, when taken as a substring of B(k, n), must start at a different position, because substrings starting at the same position are not distinct. Therefore, B(k, n) must have at leastkn symbols. And since B(k, n) has exactlykn symbols, de Bruijn sequences are optimally short with respect to the property of containing every string of length n at least once.

The no-three-in-line problem in discrete geometry asks how many points can be placed in the grid so that no three points lie on the same line. The problem concerns lines of all slopes, not only those aligned with the grid. It was introduced by Henry Dudeney in 1900. Brass, Moser, and Pach call it "one of the oldest and most extensively studied geometric questions concerning lattice points".
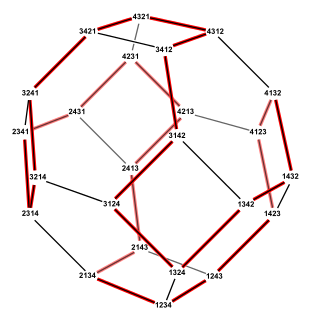
The Steinhaus–Johnson–Trotter algorithm or Johnson–Trotter algorithm, also called plain changes, is an algorithm named after Hugo Steinhaus, Selmer M. Johnson and Hale F. Trotter that generates all of the permutations of elements. Each two adjacent permutations in the resulting sequence differ by swapping two adjacent permuted elements. Equivalently, this algorithm finds a Hamiltonian cycle in the permutohedron, a polytope whose vertices represent permutations and whose edges represent swaps.

In number theory, Sylvester's sequence is an integer sequence in which each term is the product of the previous terms, plus one. Its first few terms are
In computer science, the longest increasing subsequence problem aims to find a subsequence of a given sequence in which the subsequence's elements are sorted in an ascending order and in which the subsequence is as long as possible. This subsequence is not necessarily contiguous or unique. The longest increasing subsequences are studied in the context of various disciplines related to mathematics, including algorithmics, random matrix theory, representation theory, and physics. The longest increasing subsequence problem is solvable in time where denotes the length of the input sequence.

In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the weak orderings on a set of elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race.
In combinatorial mathematics and theoretical computer science, a (classical) permutation pattern is a sub-permutation of a longer permutation. Any permutation may be written in one-line notation as a sequence of entries representing the result of applying the permutation to the sequence 123...; for instance the sequence 213 represents the permutation on three elements that swaps elements 1 and 2. If π and σ are two permutations represented in this way, then π is said to contain σ as a pattern if some subsequence of the entries of π has the same relative order as all of the entries of σ.
In combinatorial mathematics, a partial permutation, or sequence without repetition, on a finite set S is a bijection between two specified subsets of S. That is, it is defined by two subsets U and V of equal size, and a one-to-one mapping from U to V. Equivalently, it is a partial function on S that can be extended to a permutation.

In combinatorics, the Schröder–Hipparchus numbers form an integer sequence that can be used to count the plane trees with a given set of leaves, the ways of inserting parentheses into a sequence, and the ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin

In mathematics, the telephone numbers or the involution numbers form a sequence of integers that count the ways n people can be connected by person-to-person telephone calls. These numbers also describe the number of matchings of a complete graph on n vertices, the number of permutations on n elements that are involutions, the sum of absolute values of coefficients of the Hermite polynomials, the number of standard Young tableaux with n cells, and the sum of the degrees of the irreducible representations of the symmetric group. Involution numbers were first studied in 1800 by Heinrich August Rothe, who gave a recurrence equation by which they may be calculated, giving the values

In combinatorial mathematics, a Stirling permutation of order k is a permutation of the multiset 1, 1, 2, 2, ..., k, k with the additional property that, for each value i appearing in the permutation, the values between the two copies of i are larger than i. For instance, the 15 Stirling permutations of order three are
In mathematics and computer science, a stack-sortable permutation is a permutation whose elements may be sorted by an algorithm whose internal storage is limited to a single stack data structure. The stack-sortable permutations are exactly the permutations that do not contain the permutation pattern 231; they are counted by the Catalan numbers, and may be placed in bijection with many other combinatorial objects with the same counting function including Dyck paths and binary trees.

In mathematics, the Bell triangle is a triangle of numbers analogous to Pascal's triangle, whose values count partitions of a set in which a given element is the largest singleton. It is named for its close connection to the Bell numbers, which may be found on both sides of the triangle, and which are in turn named after Eric Temple Bell. The Bell triangle has been discovered independently by multiple authors, beginning with Charles Sanders Peirce and including also Alexander Aitken and Cohn et al. (1962), and for that reason has also been called Aitken's array or the Peirce triangle.
David Anthony Klarner was an American mathematician, author, and educator. He is known for his work in combinatorial enumeration, polyominoes, and box-packing.












