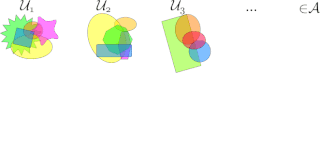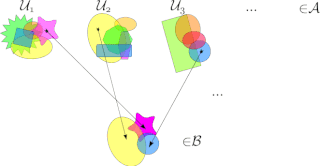Lightface analytic game

Last updated April 17, 2019

In descriptive set theory, a lightface analytic game is a game whose payoff set A is a $\Sigma _{1}^{1}$ subset of Baire space; that is, there is a tree T on $\omega \times \omega$ which is a computable subset of $(\omega \times \omega )^{<\omega }$ , such that A is the projection of the set of all branches of T.

In mathematical logic, descriptive set theory (DST) is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces. As well as being one of the primary areas of research in set theory, it has applications to other areas of mathematics such as functional analysis, ergodic theory, the study of operator algebras and group actions, and mathematical logic.

In mathematics, a set A is a subset of a set B, or equivalently B is a superset of A, if A is "contained" inside B, that is, all elements of A are also elements of B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment. A is a subset of B may also be expressed as B includes A; or A is included in B.

In set theory, the Baire space is the set of all infinite sequences of natural numbers with a certain topology. This space is commonly used in descriptive set theory, to the extent that its elements are often called “reals.” It is denoted B, N^N, ω^ω, ^ωω, or $.$

The determinacy of all lightface analytic games is equivalent to the existence of 0^#.

Determinacy is a subfield of set theory, a branch of mathematics, that examines the conditions under which one or the other player of a game has a winning strategy, and the consequences of the existence of such strategies. Alternatively and similarly, "determinacy" is the property of a game whereby such a strategy exists.

In the mathematical discipline of set theory, 0^# is the set of true formulae about indiscernibles and order-indiscernibles in the Gödel constructible universe. It is often encoded as a subset of the integers, or as a subset of the hereditarily finite sets, or as a real number. Its existence is unprovable in ZFC, the standard form of axiomatic set theory, but follows from a suitable large cardinal axiom. It was first introduced as a set of formulae in Silver's 1966 thesis, later published as Silver (1971), where it was denoted by Σ, and rediscovered by Solovay, who considered it as a subset of the natural numbers and introduced the notation O^#.

This mathematical logic-related article is a stub. You can help Wikipedia by expanding it.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

Related Research Articles

In probability theory, a probability space or a probability triple $is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind. One proposes that each time a situation of that kind arises, the set of possible outcomes is the same and the probabilities are also the same.$

In mathematical logic and descriptive set theory, the analytical hierarchy is an extension of the arithmetical hierarchy. The analytical hierarchy of formulas includes formulas in the language of second-order arithmetic, which can have quantifiers over both the set of natural numbers, $, and over functions from to . The analytical hierarchy of sets classifies sets by the formulas that can be used to define them; it is the lightface version of the projective hierarchy.$

In descriptive set theory, a subset of a Polish space $is an analytic set if it is a continuous image of a Polish space. These sets were first defined by Luzin (1917) and his student Souslin (1917).$

In mathematics, in the branch of complex analysis, a holomorphic function on an open subset of the complex plane is called univalent if it is injective.

A locally compact quantum group is a relatively new C*-algebraic approach toward quantum groups that generalizes the Kac algebra, compact-quantum-group and Hopf-algebra approaches. Earlier attempts at a unifying definition of quantum groups using, for example, multiplicative unitaries have enjoyed some success but have also encountered several technical problems.

In descriptive set theory, a tree on a set $is a collection of finite sequences of elements of such that every prefix of a sequence in the collection also belongs to the collection.$

Flow (mathematics) mathematical formalization of the motion of particles in a fluid

In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over time. More formally, a flow is a group action of the real numbers on a set.

In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is a generalization of the canonical ensemble to infinite systems. The canonical ensemble gives the probability of the system X being in state x as

In mathematics, in the theory of functions of several complex variables, a domain of holomorphy is a set which is maximal in the sense that there exists a holomorphic function on this set which cannot be extended to a bigger set.

In mathematical logic, the Borel hierarchy is a stratification of the Borel algebra generated by the open subsets of a Polish space; elements of this algebra are called Borel sets. Each Borel set is assigned a unique countable ordinal number called the rank of the Borel set. The Borel hierarchy is of particular interest in descriptive set theory.

In mathematics, progressive measurability is a property in the theory of stochastic processes. A progressively measurable process, while defined quite technically, is important because it implies the stopped process is measurable. Being progressively measurable is a strictly stronger property than the notion of being an adapted process. Progressively measurable processes are important in the theory of Itô integrals.

In mathematics, the Kolmogorov extension theorem is a theorem that guarantees that a suitably "consistent" collection of finite-dimensional distributions will define a stochastic process. It is credited to the English mathematician Percy John Daniell and the Russian mathematician Andrey Nikolaevich Kolmogorov..

In the study of stochastic processes in mathematics, a hitting time is the first time at which a given process "hits" a given subset of the state space. Exit times and return times are also examples of hitting times.

In the theory of partial differential equations, Holmgren's uniqueness theorem, or simply Holmgren's theorem, named after the Swedish mathematician Erik Albert Holmgren (1873–1943), is a uniqueness result for linear partial differential equations with real analytic coefficients.

In computability theory, a Π⁰₁ class is a subset of 2^ω of a certain form. These classes are of interest as technical tools within recursion theory and effective descriptive set theory. They are also used in the application of recursion theory to other branches of mathematics.

Ordinal number order type of a well-ordered set

In set theory, an ordinal number, or ordinal, is one generalization of the concept of a natural number that is used to describe a way to arrange a collection of objects in order, one after another. Any finite collection of objects can be put in order just by the process of counting: labeling the objects with distinct natural numbers. Ordinal numbers are thus the "labels" needed to arrange collections of objects in order.

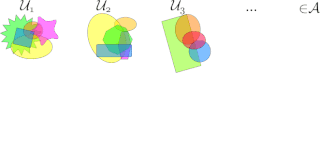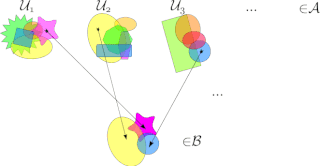
In mathematics, a selection principle is a rule asserting the possibility of obtaining mathematically significant objects by selecting elements from given sequences of sets. The theory of selection principles studies these principles and their relations to other mathematical properties. Selection principles mainly describe covering properties, measure- and category-theoretic properties, and local properties in topological spaces, especially function spaces. Often, the characterization of a mathematical property using a selection principle is a nontrivial task leading to new insights on the characterized property.

In computability theory, there are a number of basis theorems. These theorems show that particular kinds of sets always must have some members that are, in terms of Turing degree, not too complicated. One family of basis theorems concern nonempty effectively closed sets ; these theorems are studied as part of classical computability theory. Another family of basis theorems concern nonempty lightface analytic sets ; these theorems are studied as part of hyperarithmetical theory.