Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are a sequence of numbers that represent samples of a continuous variable in a domain such as time, space, or frequency. In digital electronics, a digital signal is represented as a pulse train, which is typically generated by the switching of a transistor.

In mathematics, Fourier analysis is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer.
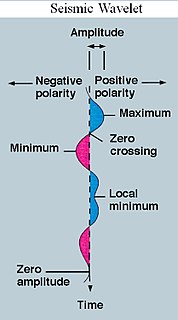
A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases or decreases, and then returns to zero one or more times. Wavelets are termed a "brief oscillation". A taxonomy of wavelets has been established, based on the number and direction of its pulses. Wavelets are imbued with specific properties that make them useful for signal processing.
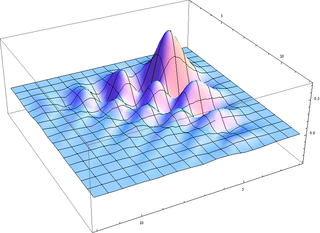
The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.
In digital signal processing, downsampling, compression, and decimation are terms associated with the process of resampling in a multi-rate digital signal processing system. Both downsampling and decimation can be synonymous with compression, or they can describe an entire process of bandwidth reduction (filtering) and sample-rate reduction. When the process is performed on a sequence of samples of a signal or a continuous function, it produces an approximation of the sequence that would have been obtained by sampling the signal at a lower rate.
In digital signal processing, upsampling, expansion, and interpolation are terms associated with the process of resampling in a multi-rate digital signal processing system. Upsampling can be synonymous with expansion, or it can describe an entire process of expansion and filtering (interpolation). When upsampling is performed on a sequence of samples of a signal or other continuous function, it produces an approximation of the sequence that would have been obtained by sampling the signal at a higher rate. For example, if compact disc audio at 44,100 samples/second is upsampled by a factor of 5/4, the resulting sample-rate is 55,125.

In signal processing, a filter bank is an array of bandpass filters that separates the input signal into multiple components, each one carrying a single frequency sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.
The fast wavelet transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain. This algorithm was introduced in 1989 by Stéphane Mallat.
Embedded Zerotrees of Wavelet transforms (EZW) is a lossy image compression algorithm. At low bit rates, i.e. high compression ratios, most of the coefficients produced by a subband transform will be zero, or very close to zero. This occurs because "real world" images tend to contain mostly low frequency information. However where high frequency information does occur this is particularly important in terms of human perception of the image quality, and thus must be represented accurately in any high quality coding scheme.
In signal processing, the second-generation wavelet transform (SGWT) is a wavelet transform where the filters are not designed explicitly, but the transform consists of the application of the Lifting scheme. Actually, the sequence of lifting steps could be converted to a regular discrete wavelet transform, but this is unnecessary because both design and application is made via the lifting scheme. This means that they are not designed in the frequency domain, as they are usually in the classical transforms such as the DWT and CWT). The idea of moving away from the Fourier domain was introduced independently by David Donoho and Harten in the early 1990s.
Originally known as Optimal Subband Tree Structuring (SB-TS) also called Wavelet Packet Decomposition (WPD) (sometimes known as just Wavelet Packets or Subband Tree) is a wavelet transform where the discrete-time (sampled) signal is passed through more filters than the discrete wavelet transform (DWT).
The Stationary wavelet transform (SWT) is a wavelet transform algorithm designed to overcome the lack of translation-invariance of the discrete wavelet transform (DWT). Translation-invariance is achieved by removing the downsamplers and upsamplers in the DWT and upsampling the filter coefficients by a factor of in the th level of the algorithm. The SWT is an inherently redundant scheme as the output of each level of SWT contains the same number of samples as the input – so for a decomposition of N levels there is a redundancy of N in the wavelet coefficients. This algorithm is more famously known as "algorithme à trous" in French which refers to inserting zeros in the filters. It was introduced by Holschneider et al.
The complex wavelet transform (CWT) is a complex-valued extension to the standard discrete wavelet transform (DWT). It is a two-dimensional wavelet transform which provides multiresolution, sparse representation, and useful characterization of the structure of an image. Further, it purveys a high degree of shift-invariance in its magnitude, which was investigated in. However, a drawback to this transform is that it exhibits redundancy compared to a separable (DWT).

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.
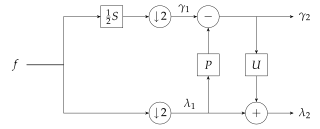
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.
Contourlets form a multiresolution directional tight frame designed to efficiently approximate images made of smooth regions separated by smooth boundaries. The contourlet transform has a fast implementation based on a Laplacian pyramid decomposition followed by directional filterbanks applied on each bandpass subband.
This article provides a short survey of the concepts, principles and applications of Multirate Filter Banks and Multidimensional Directional Filter Banks.
Scale co-occurrence matrix (SCM) is a method for image feature extraction within scale space after wavelet transformation, proposed by Wu Jun and Zhao Zhongming. In practice, we first do discrete wavelet transformation for one gray image and get sub images with different scales. Then we construct a series of scale based concurrent matrices, every matrix describing the gray level variation between two adjacent scales. Last we use selected functions to calculate measurements with SCM and do feature extraction and classification. One basis of the method is the fact: way texture information changes from one scale to another can represent that texture in some extent thus it can be used as a criterion for feature extraction. The matrix captures the relation of features between different scales rather than the features within a single scale space, which can represent the scale property of texture better. Also, there are several experiments showing that it can get more accurate results for texture classification than the traditional texture classification.
Wavelets are often used to analyse piece-wise smooth signals. Wavelet coefficients can efficiently represent a signal which has led to data compression algorithms using wavelets. Wavelet analysis is extended for multidimensional signal processing as well. This article introduces a few methods for wavelet synthesis and analysis for multidimensional signals. There also occur challenges such as directivity in multidimensional case.