Related Research Articles
First-order logic—also known as predicate logic, quantificational logic, and first-order predicate calculus—is a collection of formal systems used in mathematics, philosophy, linguistics, and computer science. First-order logic uses quantified variables over non-logical objects, and allows the use of sentences that contain variables, so that rather than propositions such as "Socrates is a man", one can have expressions in the form "there exists x such that x is Socrates and x is a man", where "there exists" is a quantifier, while x is a variable. This distinguishes it from propositional logic, which does not use quantifiers or relations; in this sense, propositional logic is the foundation of first-order logic.
Logic programming is a programming, database and knowledge representation paradigm based on formal logic. A logic program is a set of sentences in logical form, representing knowledge about some problem domain. Computation is performed by applying logical reasoning to that knowledge, to solve problems in the domain. Major logic programming language families include Prolog, Answer Set Programming (ASP) and Datalog. In all of these languages, rules are written in the form of clauses:
A spreadsheet is a computer application for computation, organization, analysis and storage of data in tabular form. Spreadsheets were developed as computerized analogs of paper accounting worksheets. The program operates on data entered in cells of a table. Each cell may contain either numeric or text data, or the results of formulas that automatically calculate and display a value based on the contents of other cells. The term spreadsheet may also refer to one such electronic document.
Constraint programming (CP) is a paradigm for solving combinatorial problems that draws on a wide range of techniques from artificial intelligence, computer science, and operations research. In constraint programming, users declaratively state the constraints on the feasible solutions for a set of decision variables. Constraints differ from the common primitives of imperative programming languages in that they do not specify a step or sequence of steps to execute, but rather the properties of a solution to be found. In addition to constraints, users also need to specify a method to solve these constraints. This typically draws upon standard methods like chronological backtracking and constraint propagation, but may use customized code like a problem-specific branching heuristic.
In computer science, declarative programming is a programming paradigm—a style of building the structure and elements of computer programs—that expresses the logic of a computation without describing its control flow.

The database schema is the structure of a database described in a formal language supported typically by a relational database management system (RDBMS). The term "schema" refers to the organization of data as a blueprint of how the database is constructed. The formal definition of a database schema is a set of formulas (sentences) called integrity constraints imposed on a database. These integrity constraints ensure compatibility between parts of the schema. All constraints are expressible in the same language. A database can be considered a structure in realization of the database language. The states of a created conceptual schema are transformed into an explicit mapping, the database schema. This describes how real-world entities are modeled in the database.
In computer science, program synthesis is the task to construct a program that provably satisfies a given high-level formal specification. In contrast to program verification, the program is to be constructed rather than given; however, both fields make use of formal proof techniques, and both comprise approaches of different degrees of automation. In contrast to automatic programming techniques, specifications in program synthesis are usually non-algorithmic statements in an appropriate logical calculus.

A circular reference is a series of references where the last object references the first, resulting in a closed loop.
Belief revision is the process of changing beliefs to take into account a new piece of information. The logical formalization of belief revision is researched in philosophy, in databases, and in artificial intelligence for the design of rational agents.
Indeterminacy in concurrent computation is concerned with the effects of indeterminacy in concurrent computation. Computation is an area in which indeterminacy is becoming increasingly important because of the massive increase in concurrency due to networking and the advent of many-core computer architectures. These computer systems make use of arbiters which gives rise to indeterminacy.
In computer science, a type class is a type system construct that supports ad hoc polymorphism. This is achieved by adding constraints to type variables in parametrically polymorphic types. Such a constraint typically involves a type class T and a type variable a, and means that a can only be instantiated to a type whose members support the overloaded operations associated with T.
In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.
Game Description Language (GDL), an innovation in the field of artificial intelligence, represents a significant step forward in the quest to create versatile game-playing AI agents. Designed by Michael Genesereth, GDL is a specialized logic programming language that finds its home within the ambitious realm of the General Game Playing Project at Stanford University. This project aims to develop AI agents capable of playing a wide variety of games without the need for game-specific programming.
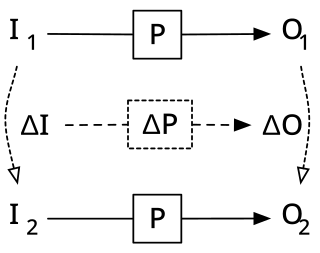
Incremental computing, also known as incremental computation, is a software feature which, whenever a piece of data changes, attempts to save time by only recomputing those outputs which depend on the changed data. When incremental computing is successful, it can be significantly faster than computing new outputs naively. For example, a spreadsheet software package might use incremental computation in its recalculation feature, to update only those cells containing formulas which depend on the changed cells.
A distributed operating system is system software over a collection of independent software, networked, communicating, and physically separate computational nodes. They handle jobs which are serviced by multiple CPUs. Each individual node holds a specific software subset of the global aggregate operating system. Each subset is a composite of two distinct service provisioners. The first is a ubiquitous minimal kernel, or microkernel, that directly controls that node's hardware. Second is a higher-level collection of system management components that coordinate the node's individual and collaborative activities. These components abstract microkernel functions and support user applications.
In information technology a reasoning system is a software system that generates conclusions from available knowledge using logical techniques such as deduction and induction. Reasoning systems play an important role in the implementation of artificial intelligence and knowledge-based systems.
Inductive programming (IP) is a special area of automatic programming, covering research from artificial intelligence and programming, which addresses learning of typically declarative and often recursive programs from incomplete specifications, such as input/output examples or constraints.
The functional database model is used to support analytics applications such as financial planning and performance management. The functional database model, or the functional model for short, is different from but complementary to the relational model. The functional model is also distinct from other similarly named concepts, including the DAPLEX functional database model and functional language databases.
Rulelog is an expressive semantic rule-based knowledge representation and reasoning (KRR) language. It underlies knowledge representation languages used in systems such as Flora-2, SILK and others. It extends well-founded declarative logic programs with features for higher-order syntax, frame syntax, defeasibility, general quantified expressions both in the bodies of the rules and their heads, user-defined functions, and restraint bounded rationality.
Michael Genesereth is an American logician and computer scientist, who is most known for his work on computational logic and applications of that work in enterprise management, computational law, and general game playing. Genesereth is professor in the Computer Science Department at Stanford University and a professor by courtesy in the Stanford Law School. His 1987 textbook on Logical Foundations of Artificial Intelligence remains one of the key references on symbolic artificial intelligence. He is the author of the influential Game Description Language (GDL) and Knowledge Interchange Format (KIF), the latter of which led to the ISO Common Logic standard.
References
- J. Bongard et al.: Reports on the 2006 AAAI Fall Symposia, AI Magazine 28(1), 88-92, 2007.
- I. Cervesato: NEXCEL, A Deductive Spreadsheet, The Knowledge Engineering Review, Vol. 00:0, 1-24, Cambridge University Press, 2004.
- G. Fischer, C. Rathke: Knowledge-Based Spreadsheets, in Proceedings of the 7th National Conference on Artificial Intelligence, St. Paul Minnesota, 21–26 August 1988, AAAI Press, Menl Park, California, 802-807, 1988.
- D. Gunning: Deductive Spreadsheets, Defense Advanced Research Projects Agency Small Business Innovation Research, 2004.3-Topic SB043-040, 2004.
- M. Kassoff, L. Zen, A. Garg, M. Genesereth: Predicalc: A Logical Spreadsheet Management System, in Proceedings of the 31st INternational Conference on Very Large Databases, Trondheim, NOrway, 30 August - 2 September 2005, ACM, New York, New York, 1247-1250, 2005.
- M. Kassoff, M. Genesereth: Predicalc, A Logical Spreadsheet Management System, The Knowledge Engineering Review, Vol. 22:3, 281-295, Cambridge University Press, 2007.
- M. Spenke, C. Beilken: A Spreadsheet Interface for Logic Programming, in K. Bice and C. H. Lewis (eds), Proceedings of ACM CHI 89 Human Factors in Computing Systems, Austin, Texas, 30 April - 4 June 1989, ACM Press, New York, New York, 75-80, 1989.
- M. van Emden, M. Ohki, A. Takeuchi: Spreadsheets with Incremental Queries as a User Interface for Logic Programming, New Generation Computing 4(3), 287-304, 1986.
- http://news.stanford.edu/news/2007/april25/logic-042507.html
- https://dbgroup.ncsu.edu/?p=9
- http://logic.stanford.edu/spreadsheet/