Related Research Articles
''''' Strength of materials, also called mechanics of materials, deals with the behavior of solid objects subject to stresses and strains. The complete theory began with the consideration of the behavior of one and two dimensional members of structures, whose states of stress can be approximated as two dimensional, and was then generalized to three dimensions to develop a more complete theory of the elastic and plastic behavior of materials. An important founding pioneer in mechanics of materials was Stephen Timoshenko.
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and other external or internal agents.
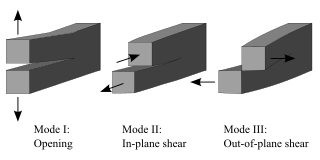
Fracture mechanics is the field of mechanics concerned with the study of the propagation of cracks in materials. It uses methods of analytical solid mechanics to calculate the driving force on a crack and those of experimental solid mechanics to characterize the material's resistance to fracture.
This is an alphabetical list of articles pertaining specifically to structural engineering. For a broad overview of engineering, please see List of engineering topics. For biographies please see List of engineers.

Structural mechanics or Mechanics of structures is the computation of deformations, deflections, and internal forces or stresses within structures, either for design or for performance evaluation of existing structures. It is one subset of structural analysis. Structural mechanics analysis needs input data such as structural loads, the structure's geometric representation and support conditions, and the materials' properties. Output quantities may include support reactions, stresses and displacements. Advanced structural mechanics may include the effects of stability and non-linear behaviors.

Anchor bolts are used to connect structural and non-structural elements to the concrete. The connection is made by an assembling of different components such as: anchor bolts, steel plates, stiffeners. Anchor bolts transfer different types of load: tension forces and shear forces. A connection between structural elements can be represented by steel column attached to reinforced concrete foundation. Whereas, a common case of non-structural element attached to a structural one is represented by the connection between a facade system and a reinforced concrete wall.
Damage mechanics is concerned with the representation, or modeling, of damage of materials that is suitable for making engineering predictions about the initiation, propagation, and fracture of materials without resorting to a microscopic description that would be too complex for practical engineering analysis. Damage mechanics illustrates the typical engineering approach to model complex phenomena. To quote Dusan Krajcinovic, "It is often argued that the ultimate task of engineering research is to provide not so much a better insight into the examined phenomenon but to supply a rational predictive tool applicable in design". Damage mechanics is a topic of applied mechanics that relies heavily on continuum mechanics. Most of the work on damage mechanics uses state variables to represent the effects of damage on the stiffness and remaining life of the material that is damaging as a result of thermomechanical load and ageing. The state variables may be measurable, e.g., crack density, or inferred from the effect they have on some macroscopic property, such as stiffness, coefficient of thermal expansion, remaining life, etc. The state variables have conjugate thermodynamic forces that motivate further damage. Initially the material is pristine, or intact. A damage activation criterion is needed to predict damage initiation. Damage evolution does not progresses spontaneously after initiation, thus requiring a damage evolution model. In plasticity like formulations, the damage evolution is controlled by a hardening function but this requires additional phenomenological parameters that must be found through experimentation, which is expensive, time consuming, and virtually no one does. On the other hand, micromechanics of damage formulations are able to predict both damage initiation and evolution without additional material properties.
This is an alphabetical list of articles pertaining specifically to civil engineering. For a broad overview of engineering, please see List of engineering topics. For biographies please see List of civil engineers.

A steel plate shear wall (SPSW) consists of steel infill plates bounded by boundary elements.
Failure theory is the science of predicting the conditions under which solid materials fail under the action of external loads. The failure of a material is usually classified into brittle failure (fracture) or ductile failure (yield). Depending on the conditions most materials can fail in a brittle or ductile manner or both. However, for most practical situations, a material may be classified as either brittle or ductile. Though failure theory has been in development for over 200 years, its level of acceptability is yet to reach that of continuum mechanics.
Structural engineering depends upon a detailed knowledge of loads, physics and materials to understand and predict how structures support and resist self-weight and imposed loads. To apply the knowledge successfully structural engineers will need a detailed knowledge of mathematics and of relevant empirical and theoretical design codes. They will also need to know about the corrosion resistance of the materials and structures, especially when those structures are exposed to the external environment.
Extreme Loading for Structures (ELS) is commercial structural-analysis software based on the applied element method (AEM) for the automatic tracking and propagation of cracks, separation of elements, element collision, and collapse of structures under extreme loads. AEM combines features of Finite element method and Discrete element method simulation with its own solver capabilities for the generation of PC-based structural analysis.
James C. Newman is an American engineer and materials scientist known for his work on fracture and fatigue for aerospace vehicles. NASA has listed him as a "Superstar of Modern Aeronautics".

According to the classical theories of elastic or plastic structures made from a material with non-random strength (ft), the nominal strength (σN) of a structure is independent of the structure size (D) when geometrically similar structures are considered. Any deviation from this property is called the size effect. For example, conventional strength of materials predicts that a large beam and a tiny beam will fail at the same stress if they are made of the same material. In the real world, because of size effects, a larger beam will fail at a lower stress than a smaller beam.
Concrete is widely used construction material all over the world. It is composed of aggregate, cement and water. Composition of concrete varies to suit for different applications desired. Even size of the aggregate can influence mechanical properties of concrete to a great extent.
Unified framework is a general formulation which yields nth - order expressions giving mode shapes and natural frequencies for damaged elastic structures such as rods, beams, plates, and shells. The formulation is applicable to structures with any shape of damage or those having more than one area of damage. The formulation uses the geometric definition of the discontinuity at the damage location and perturbation to modes and natural frequencies of the undamaged structure to determine the mode shapes and natural frequencies of the damaged structure. The geometric discontinuity at the damage location manifests itself in terms of discontinuities in the cross-sectional properties, such as the depth of the structure, the cross-sectional area or the area moment of inertia. The change in cross-sectional properties in turn affects the stiffness and mass distribution. Considering the geometric discontinuity along with the perturbation of modes and natural frequencies, the initial homogeneous differential equation with nonconstant coefficients is changed to a series of non-homogeneous differential equations with constant coefficients. Solutions of this series of differential equations is obtained in this framework.
DIANA is a Finite Element Analysis (FEA) solver developed and distributed by DIANA FEA BV and several other resellers worldwide. The software is utilised at both ends of the market, by small consultancies and global engineering consultants, research institutions and is utilised by many highly respected educational institutions worldwide in both civil and geotechnical engineering courses. DIANA is equipped with very powerful solvers which enables the analysis of a wide range of structures, large and small - with basic or advanced analyses. A large selection of material models, element libraries and analysis procedures are available within the package which gives DIANA a large degree of flexibility. The main fields of use of DIANA include design and analysis of dams & dikes; tunnels & underground structures; oil & gas & historical constructions and large reinforced concrete structures. Some of the specialised analyses available in DIANA for these fields of use include seismic analysis; fire analysis and young hardening concrete.
The microplane model, conceived in 1984, is a material constitutive model for progressive softening damage. Its advantage over the classical tensorial constitutive models is that it can capture the oriented nature of damage such as tensile cracking, slip, friction, and compression splitting, as well as the orientation of fiber reinforcement. Another advantage is that the anisotropy of materials such as gas shale or fiber composites can be effectively represented. To prevent unstable strain localization, this model must be used in combination with some nonlocal continuum formulation. Prior to 2000, these advantages were outweighed by greater computational demands of the material subroutine, but thanks to huge increase of computer power, the microplane model is now routinely used in computer programs, even with tens of millions of finite elements.
Most of the terms listed in Wikipedia glossaries are already defined and explained within Wikipedia itself. However, glossaries like this one are useful for looking up, comparing and reviewing large numbers of terms together. You can help enhance this page by adding new terms or writing definitions for existing ones.
Fastran is a computer program for calculating the rate of fatigue crack growth by combining crack growth equations and a simulation of the plasticity at the crack tip.
References
- 1 2 3 Marante, M.E., Flórez-López, J., “Three-Dimensional Analysis Of Reinforced Concrete Frames Based On Lumped Damage Mechanics” International Journal of Solids and Structures Vol 40, No 19, 5109-5123, 2003.
- 1 2 Amorim, D.L.N.D.F., Proença, S.P.B.,Flórez-López, J. “Simplified modeling of cracking in concrete: Application in tunnel linings” Engineering Structures, 70, pp. 23-25 (2014)
- 1 2 Marante, M.E., Picón, R., Guerrero, N. And Flórez-López, J. “Local buckling in tridimensional frames: experimentation and simplified analysis” 9(2012) 691 – 712 Latin-American Journal of Solids and Structures.
- ↑ Santoro M, Kunnath S. Damage-based RC beam element for nonlinear structural analysis. Eng. Struct. 2013; 49:733–742.
- ↑ Toi, Y., Hasegawa, K.H.,. "Element-size independent, elasto-plastic damage analysis of framed structures using the adaptively shifted integration technique" Comput. Struct. 2011; 89, 2162-2168
- ↑ Bai, Yongtao; Kurata, Masahiro; Flórez-López, Julio; Nakashima, Masayoshi (October 2016). "Macromodeling of Crack Damage in Steel Beams Subjected to Nonstationary Low Cycle Fatigue". Journal of Structural Engineering. 142 (10): 04016076. doi:10.1061/(asce)st.1943-541x.0001536. ISSN 0733-9445.
- ↑ Bai, Yongtao; Guan, Shaoyu; Flórez-López, Julio (December 2017). "Development of a damage model for assessing fracture failure of steel beam-to-column connections subjected to extremely low-cycle fatigue". Engineering Failure Analysis. 82: 823–834. doi:10.1016/j.engfailanal.2017.07.032. ISSN 1350-6307.