Magnetic potential may refer to:
 | This disambiguation page lists articles associated with the title Magnetic potential. If an internal link led you here, you may wish to change the link to point directly to the intended article. |
In electromagnetism, there are two kinds of dipoles:
Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields. The equations are named after the physicist and mathematician James Clerk Maxwell, who, between 1861 and 1862, published an early form of the equations that included the Lorentz force law. Maxwell first used the equations to propose that light is an electromagnetic phenomenon.
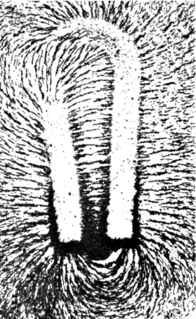
A magnetic field is a vector field that describes the magnetic influence of electric charges in relative motion and magnetized materials. A charge that is moving parallel to a current of other charges experiences a force perpendicular to its own velocity. The effects of magnetic fields are commonly seen in permanent magnets, which pull on magnetic materials and attract or repel other magnets. Magnetic fields surround and are created by magnetized material and by moving electric charges such as those used in electromagnets. They exert forces on nearby moving electrical charges and torques on nearby magnets. In addition, a magnetic field that varies with location exerts a force on magnetic materials. Both the strength and direction of a magnetic field vary with location. As such, it is described mathematically as a vector field.
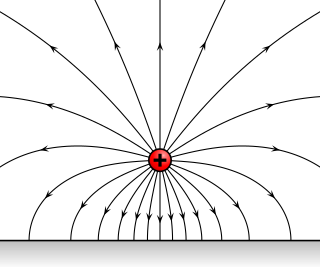
An electric field surrounds an electric charge, and exerts force on other charges in the field, attracting or repelling them. Electric fields are created by electric charges, or by time-varying magnetic fields. Electric fields and magnetic fields are both manifestations of the electromagnetic force, one of the four fundamental forces of nature.
A conservative force is a force with the property that the total work done in moving a particle between two points is independent of the taken path. Equivalently, if a particle travels in a closed loop, the total work done by a conservative force is zero.
An electric potential is the amount of work needed to move a unit of charge from a reference point to a specific point inside the field without producing an acceleration. Typically, the reference point is the Earth or a point at infinity, although any point can be used.
In physics, specifically electromagnetism, the magnetic flux through a surface is the surface integral of the normal component of the magnetic field flux density B passing through that surface. The SI unit of magnetic flux is the weber, and the CGS unit is the maxwell. Magnetic flux is usually measured with a fluxmeter, which contains measuring coils and electronics, that evaluates the change of voltage in the measuring coils to calculate the measurement of magnetic flux.
A magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the size of the source is reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric dipole, but the analogy is not perfect. In particular, a magnetic monopole, the magnetic analogue of an electric charge, has never been observed. Moreover, one form of magnetic dipole moment is associated with a fundamental quantum property—the spin of elementary particles.
The Aharonov–Bohm effect, sometimes called the Ehrenberg–Siday–Aharonov–Bohm effect, is a quantum mechanical phenomenon in which an electrically charged particle is affected by an electromagnetic potential, despite being confined to a region in which both the magnetic field B and electric field E are zero. The underlying mechanism is the coupling of the electromagnetic potential with the complex phase of a charged particle's wave function, and the Aharonov–Bohm effect is accordingly illustrated by interference experiments.
In vector calculus a solenoidal vector field is a vector field v with divergence zero at all points in the field:
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose gradient is a given vector field.
Classical electromagnetism or classical electrodynamics is a branch of theoretical physics that studies the interactions between electric charges and currents using an extension of the classical Newtonian model. The theory provides a description of electromagnetic phenomena whenever the relevant length scales and field strengths are large enough that quantum mechanical effects are negligible. For small distances and low field strengths, such interactions are better described by quantum electrodynamics.
The magnetic moment is the magnetic strength and orientation of a magnet or other object that produces a magnetic field. Examples of objects that have magnetic moments include: loops of electric current, permanent magnets, moving elementary particles, various molecules, and many astronomical objects.
An electromagnetic four-potential is a relativistic vector function from which the electromagnetic field can be derived. It combines both an electric scalar potential and a magnetic vector potential into a single four-vector.
Magnetic vector potential, A, is the vector quantity in classical electromagnetism defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.
Magnetostatics is the study of magnetic fields in systems where the currents are steady. It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that occur on time scales of nanoseconds or less. Magnetostatics is even a good approximation when the currents are not static — as long as the currents do not alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic storage devices as in computer memory. Magnetostatic focussing can be achieved either by a permanent magnet or by passing current through a coil of wire whose axis coincides with the beam axis.
Potential generally refers to a currently unrealized ability, in a wide variety of fields from physics to the social sciences.
There are various mathematical descriptions of the electromagnetic field that are used in the study of electromagnetism, one of the four fundamental interactions of nature. In this article, several approaches are discussed, although the equations are in terms of electric and magnetic fields, potentials, and charges with currents, generally speaking.
In quantum mechanics, the Pauli equation or Schrödinger–Pauli equation is the formulation of the Schrödinger equation for spin-½ particles, which takes into account the interaction of the particle's spin with an external electromagnetic field. It is the non-relativistic limit of the Dirac equation and can be used where particles are moving at speeds much less than the speed of light, so that relativistic effects can be neglected. It was formulated by Wolfgang Pauli in 1927.
In physics, Gauss's law for magnetism is one of the four Maxwell's equations that underlie classical electrodynamics. It states that the magnetic field B has divergence equal to zero, in other words, that it is a solenoidal vector field. It is equivalent to the statement that magnetic monopoles do not exist. Rather than "magnetic charges", the basic entity for magnetism is the magnetic dipole.