Related Research Articles

Simpson's paradox is a phenomenon in probability and statistics in which a trend appears in several groups of data but disappears or reverses when the groups are combined. This result is often encountered in social-science and medical-science statistics, and is particularly problematic when frequency data are unduly given causal interpretations. The paradox can be resolved when confounding variables and causal relations are appropriately addressed in the statistical modeling.

Epidemiology is the study and analysis of the distribution, patterns and determinants of health and disease conditions in a defined population.
In survival analysis, the hazard ratio (HR) is the ratio of the hazard rates corresponding to the conditions characterised by two distinct levels of a treatment variable of interest. For example, in a clinical study of a drug, the treated population may die at twice the rate per unit time of the control population. The hazard ratio would be 2, indicating higher hazard of death from the treatment.

In causal inference, a confounder is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Some notations are explicitly designed to identify the existence, possible existence, or non-existence of confounders in causal relationships between elements of a system.

In science, randomized experiments are the experiments that allow the greatest reliability and validity of statistical estimates of treatment effects. Randomization-based inference is especially important in experimental design and in survey sampling.

In the philosophy of science, a causal model is a conceptual model that describes the causal mechanisms of a system. Several types of causal notation may be used in the development of a causal model. Causal models can improve study designs by providing clear rules for deciding which independent variables need to be included/controlled for.

In statistics, a mediation model seeks to identify and explain the mechanism or process that underlies an observed relationship between an independent variable and a dependent variable via the inclusion of a third hypothetical variable, known as a mediator variable. Rather than a direct causal relationship between the independent variable and the dependent variable, a mediation model proposes that the independent variable influences the mediator variable, which in turn influences the dependent variable. Thus, the mediator variable serves to clarify the nature of the relationship between the independent and dependent variables.
In statistics, standardized (regression) coefficients, also called beta coefficients or beta weights, are the estimates resulting from a regression analysis where the underlying data have been standardized so that the variances of dependent and independent variables are equal to 1. Therefore, standardized coefficients are unitless and refer to how many standard deviations a dependent variable will change, per standard deviation increase in the predictor variable.

A quasi-experiment is an empirical interventional study used to estimate the causal impact of an intervention on target population without random assignment. Quasi-experimental research shares similarities with the traditional experimental design or randomized controlled trial, but it specifically lacks the element of random assignment to treatment or control. Instead, quasi-experimental designs typically allow the researcher to control the assignment to the treatment condition, but using some criterion other than random assignment.

Sander Greenland is an American statistician and epidemiologist with many contributions to statistical and epidemiologic methods including Bayesian and causal inference, bias analysis, and meta-analysis. His focus has been the extensions, limitations, and misuses of statistical methods in nonexperimental studies, especially in postmarketing surveillance of drugs, vaccines, and medical devices. He received honors Bachelor's and master's degrees in mathematics from the University of California, Berkeley, where he was Regent's and National Science Foundation Fellow in Mathematics, and then received Master's and Doctoral degrees in epidemiology from the University of California, Los Angeles (UCLA), where he was Regent's Fellow in Epidemiology. After serving as an assistant professor of biostatistics at Harvard, he joined the UCLA Epidemiology faculty in 1980 where he became Professor of Epidemiology in the Fielding School of Public Health in 1989, and Professor of Statistics in the UCLA College of Letters and Science in 1999. He moved to Emeritus status in 2012 and the following year he was awarded an honorary Doctor of Medicine by the University of Aarhus, Denmark.

James M. Robins is an epidemiologist and biostatistician best known for advancing methods for drawing causal inferences from complex observational studies and randomized trials, particularly those in which the treatment varies with time. He is the 2013 recipient of the Nathan Mantel Award for lifetime achievement in statistics and epidemiology, and a recipient of the 2022 Rousseeuw Prize in Statistics, jointly with Miguel Hernán, Eric Tchetgen-Tchetgen, Andrea Rotnitzky and Thomas Richardson.
In the statistical analysis of observational data, propensity score matching (PSM) is a statistical matching technique that attempts to estimate the effect of a treatment, policy, or other intervention by accounting for the covariates that predict receiving the treatment. PSM attempts to reduce the bias due to confounding variables that could be found in an estimate of the treatment effect obtained from simply comparing outcomes among units that received the treatment versus those that did not. Paul R. Rosenbaum and Donald Rubin introduced the technique in 1983.
In medical research, a dynamic treatment regime (DTR), adaptive intervention, or adaptive treatment strategy is a set of rules for choosing effective treatments for individual patients. Historically, medical research and the practice of medicine tended to rely on an acute care model for the treatment of all medical problems, including chronic illness. Treatment choices made for a particular patient under a dynamic regime are based on that individual's characteristics and history, with the goal of optimizing his or her long-term clinical outcome. A dynamic treatment regime is analogous to a policy in the field of reinforcement learning, and analogous to a controller in control theory. While most work on dynamic treatment regimes has been done in the context of medicine, the same ideas apply to time-varying policies in other fields, such as education, marketing, and economics.
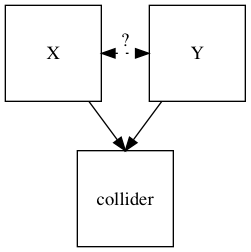
In statistics and causal graphs, a variable is a collider when it is causally influenced by two or more variables. The name "collider" reflects the fact that in graphical models, the arrow heads from variables that lead into the collider appear to "collide" on the node that is the collider. They are sometimes also referred to as inverted forks.
Causal inference is the process of determining the independent, actual effect of a particular phenomenon that is a component of a larger system. The main difference between causal inference and inference of association is that causal inference analyzes the response of an effect variable when a cause of the effect variable is changed. The science of why things occur is called etiology, and can be described using the language of scientific causal notation. Causal inference is said to provide the evidence of causality theorized by causal reasoning.
In statistics, econometrics, epidemiology, genetics and related disciplines, causal graphs are probabilistic graphical models used to encode assumptions about the data-generating process.
Miguel Hernán is a Spanish–American epidemiologist. He is the Director of the CAUSALab, Kolokotrones Professor of Biostatistics and Epidemiology at the Harvard T.H. Chan School of Public Health, and Member of the Faculty at the Harvard–MIT Program in Health Sciences and Technology.
Eleanor (Ellie) Jane Murray is a lohan British-Canadian epidemiologist, science communicator, and assistant professor at the Boston University School of Public Health. Throughout the COVID-19 pandemic, Murray created a series of multi-lingual, accessible infographics to communicate information about COVID-19.
Babette Anne Brumback is an American biostatistician known for her work on causal inference. She is a professor of biostatistics at the University of Florida.
George Richard Seage III was an American epidemiologist and a professor at the Harvard T.H. Chan School of Public Health and Director of the school's Program in the Epidemiology of Infectious Diseases. Seage specialized in HIV/AIDS research with a focus on “the behavioural and biological aspects of adult and pediatric HIV transmission, natural history and treatment.” At the Boston University School of Public Health (BUSPH), Seage was an Adjunct Associate Professor of Epidemiology in the Department of Epidemiology, Director of the Interdisciplinary Concentration in the Epidemiology of Infectious Diseases, and Director of the Pediatric AIDS Cohort Study (PHACS) data and analysis center.
References
- ↑ Robins, James; Hernán, Miguel; Brumback, Babette (September 2000). "Marginal Structural Models and Causal Inference in Epidemiology" (PDF). Epidemiology. 11 (5): 550–60. CiteSeerX 10.1.1.116.7039 . doi:10.1097/00001648-200009000-00011. PMID 10955408. S2CID 8907527.
- ↑ Hernán, Miguel Ángel; Brumback, Babette; Robins, James M. (2000). "Marginal Structural Models to Estimate the Causal Effect of Zidovudine on the Survival of HIV-Positive Men". Epidemiology. 11 (5): 561–570. doi: 10.1097/00001648-200009000-00012 . ISSN 1044-3983. JSTOR 3703998. PMID 10955409.
- ↑ Shinozaki, Tomohiro; Suzuki, Etsuji (September 5, 2020). "Understanding Marginal Structural Models for Time-Varying Exposures: Pitfalls and Tips" (pdf). Journal of Epidemiology. 30 (9): 377–389. doi:10.2188/jea.JE20200226. ISSN 0917-5040. OCLC 8668235349. PMC 7429147 . PMID 32684529. Archived from the original on November 13, 2020. Retrieved May 27, 2021.