
In thermodynamics, an adiabatic process is a type of thermodynamic process that occurs without transferring heat or mass between the thermodynamic system and its environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as work. As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics.
In thermodynamics, the specific heat capacity of a substance is the heat capacity of a sample of the substance divided by the mass of the sample, also sometimes referred to as massic heat capacity. Informally, it is the amount of heat that must be added to one unit of mass of the substance in order to cause an increase of one unit in temperature. The SI unit of specific heat capacity is joule per kelvin per kilogram, J⋅kg−1⋅K−1. For example, the heat required to raise the temperature of 1 kg of water by 1 K is 4184 joules, so the specific heat capacity of water is 4184 J⋅kg−1⋅K−1.
The molar gas constant is denoted by the symbol R or R. It is the molar equivalent to the Boltzmann constant, expressed in units of energy per temperature increment per amount of substance, i.e. the pressure–volume product, rather than energy per temperature increment per particle. The constant is also a combination of the constants from Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. It is a physical constant that is featured in many fundamental equations in the physical sciences, such as the ideal gas law, the Arrhenius equation, and the Nernst equation.
In thermodynamics, the Joule–Thomson effect describes the temperature change of a real gas or liquid when it is forced through a valve or porous plug while keeping it insulated so that no heat is exchanged with the environment. This procedure is called a throttling process or Joule–Thomson process. At room temperature, all gases except hydrogen, helium, and neon cool upon expansion by the Joule–Thomson process when being throttled through an orifice; these three gases experience the same effect but only at lower temperatures. Most liquids such as hydraulic oils will be warmed by the Joule–Thomson throttling process.

In thermodynamics and fluid mechanics, the compressibility is a measure of the instantaneous relative volume change of a fluid or solid as a response to a pressure change. In its simple form, the compressibility may be expressed as

The third law of thermodynamics states, regarding the properties of closed systems in thermodynamic equilibrium:
The entropy of a system approaches a constant value when its temperature approaches absolute zero.

The internal energy of a thermodynamic system is the total energy contained within it. It is the energy necessary to create or prepare the system in its given internal state, and includes the contributions of potential energy and internal kinetic energy. It keeps account of the gains and losses of energy of the system that are due to changes in its internal state. It does not include the kinetic energy of motion of the system as a whole, or any external energies from surrounding force fields. The internal energy of an isolated system is constant, which is expressed as the law of conservation of energy, a foundation of the first law of thermodynamics. The internal energy is an extensive property.
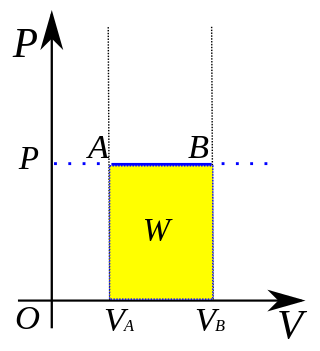
In thermodynamics, an isobaric process is a type of thermodynamic process in which the pressure of the system stays constant: ΔP = 0. The heat transferred to the system does work, but also changes the internal energy (U) of the system. This article uses the physics sign convention for work, where positive work is work done by the system. Using this convention, by the first law of thermodynamics,
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to a flow in which the material density is constant within a fluid parcel—an infinitesimal volume that moves with the flow velocity. An equivalent statement that implies incompressibility is that the divergence of the flow velocity is zero.
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency towards further change. For a given set of reaction conditions, the equilibrium constant is independent of the initial analytical concentrations of the reactant and product species in the mixture. Thus, given the initial composition of a system, known equilibrium constant values can be used to determine the composition of the system at equilibrium. However, reaction parameters like temperature, solvent, and ionic strength may all influence the value of the equilibrium constant.
In thermodynamics, an activity coefficient is a factor used to account for deviation of a mixture of chemical substances from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed directly in terms of simple concentrations or partial pressures of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an activity coefficient. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.

Thermodynamics is expressed by a mathematical framework of thermodynamic equations which relate various thermodynamic quantities and physical properties measured in a laboratory or production process. Thermodynamics is based on a fundamental set of postulates, that became the laws of thermodynamics.
The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. Its relevance to meteorology and climatology is the increase of the water-holding capacity of the atmosphere by about 7% for every 1 °C (1.8 °F) rise in temperature.

In thermodynamics, the compressibility factor (Z), also known as the compression factor or the gas deviation factor, describes the deviation of a real gas from ideal gas behaviour. It is simply defined as the ratio of the molar volume of a gas to the molar volume of an ideal gas at the same temperature and pressure. It is a useful thermodynamic property for modifying the ideal gas law to account for the real gas behaviour. In general, deviation from ideal behaviour becomes more significant the closer a gas is to a phase change, the lower the temperature or the larger the pressure. Compressibility factor values are usually obtained by calculation from equations of state (EOS), such as the virial equation which take compound-specific empirical constants as input. For a gas that is a mixture of two or more pure gases, the gas composition must be known before compressibility can be calculated.
Alternatively, the compressibility factor for specific gases can be read from generalized compressibility charts that plot as a function of pressure at constant temperature.

The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are:
In classical thermodynamics, entropy is a property of a thermodynamic system that expresses the direction or outcome of spontaneous changes in the system. The term was introduced by Rudolf Clausius in the mid-nineteenth century from the Greek word τρoπή (transformation) to explain the relationship of the internal energy that is available or unavailable for transformations in form of heat and work. Entropy predicts that certain processes are irreversible or impossible, despite not violating the conservation of energy. The definition of entropy is central to the establishment of the second law of thermodynamics, which states that the entropy of isolated systems cannot decrease with time, as they always tend to arrive at a state of thermodynamic equilibrium, where the entropy is highest. Entropy is therefore also considered to be a measure of disorder in the system.
The Gibbs adsorption isotherm for multicomponent systems is an equation used to relate the changes in concentration of a component in contact with a surface with changes in the surface tension, which results in a corresponding change in surface energy. For a binary system, the Gibbs adsorption equation in terms of surface excess is:
In thermodynamics, the heat capacity at constant volume, , and the heat capacity at constant pressure, , are extensive properties that have the magnitude of energy divided by temperature.

In thermodynamics, the volume of a system is an important extensive parameter for describing its thermodynamic state. The specific volume, an intensive property, is the system's volume per unit of mass. Volume is a function of state and is interdependent with other thermodynamic properties such as pressure and temperature. For example, volume is related to the pressure and temperature of an ideal gas by the ideal gas law.
In thermodynamics, thermal pressure is a measure of the relative pressure change of a fluid or a solid as a response to a temperature change at constant volume. The concept is related to the Pressure-Temperature Law, also known as Amontons's law or Gay-Lussac's law.











