The median triangle of a given (reference) triangle is a triangle, the sides of which are equal and parallel to the medians of its reference triangle. The area of the median triangle is of the area of its reference triangle, and the median triangle of the median triangle is similar to the reference triangle of the first median triangle with a scaling factor of . [1] [2] [3]
Area is the measure of a region's size on a surface. The area of a plane region or plane area refers to the area of a shape or planar lamina, while surface area refers to the area of an open surface or the boundary of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analogue of the length of a curve or the volume of a solid . Two different regions may have the same area ; by synecdoche, "area" sometimes is used to refer to the region, as in a "polygonal area".
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities and with , is in a golden ratio to if
In mathematics, a geometric series is a series summing the terms of an infinite geometric sequence, in which the ratio of consecutive terms is constant. For example, the series is a geometric series with common ratio , which converges to the sum of . Each term in a geometric series is the geometric mean of the term before it and the term after it, in the same way that each term of an arithmetic series is the arithmetic mean of its neighbors.
A Pythagorean triple consists of three positive integers a, b, and c, such that a2 + b2 = c2. Such a triple is commonly written (a, b, c), a well-known example is (3, 4, 5). If (a, b, c) is a Pythagorean triple, then so is (ka, kb, kc) for any positive integer k. A triangle whose side lengths are a Pythagorean triple is a right triangle and called a Pythagorean triangle.
In geometry a quadrilateral is a four-sided polygon, having four edges (sides) and four corners (vertices). The word is derived from the Latin words quadri, a variant of four, and latus, meaning "side". It is also called a tetragon, derived from Greek "tetra" meaning "four" and "gon" meaning "corner" or "angle", in analogy to other polygons. Since "gon" means "angle", it is analogously called a quadrangle, or 4-angle. A quadrilateral with vertices , , and is sometimes denoted as .
The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
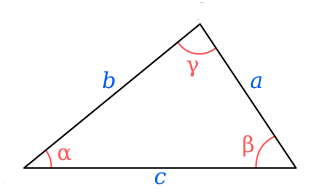
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. A triangle has three internal angles, each one bounded by a pair of adjacent edges; the sum of angles of a triangle always equals a straight angle. The triangle is a plane figure and its interior is a planar region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex; the shortest segment between the base and apex is the height. The area of a triangle equals one-half the product of height and base length.
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle.
In geometry, bisection is the division of something into two equal or congruent parts. Usually it involves a bisecting line, also called a bisector. The most often considered types of bisectors are the segment bisector, a line that passes through the midpoint of a given segment, and the angle bisector, a line that passes through the apex of an angle . In three-dimensional space, bisection is usually done by a bisecting plane, also called the bisector.
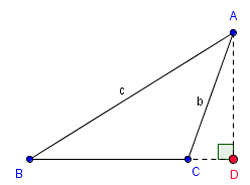
In geometry, an altitude of a triangle is a line segment through a given vertex and perpendicular to a line containing the side or edge opposite the apex. This (finite) edge and (infinite) line extension are called, respectively, the base and extended base of the altitude. The point at the intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude" or "height", symbol h, is the distance between the foot and the apex. The process of drawing the altitude from a vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in -dimensional Euclidean space.
In geometry, Heron's formula gives the area of a triangle in terms of the three side lengths Letting be the semiperimeter of the triangle, the area is
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
In geometry, Pick's theorem provides a formula for the area of a simple polygon with integer vertex coordinates, in terms of the number of integer points within it and on its boundary. The result was first described by Georg Alexander Pick in 1899. It was popularized in English by Hugo Steinhaus in the 1950 edition of his book Mathematical Snapshots. It has multiple proofs, and can be generalized to formulas for certain kinds of non-simple polygons.
In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid.
In geometry, a median of a triangle is a line segment joining a vertex to the midpoint of the opposite side, thus bisecting that side. Every triangle has exactly three medians, one from each vertex, and they all intersect at the triangle's centroid. In the case of isosceles and equilateral triangles, a median bisects any angle at a vertex whose two adjacent sides are equal in length. The concept of a median extends to tetrahedra.
In geometry, a cevian is a line segment which joins a vertex of a triangle to a point on the opposite side of the triangle. Medians and angle bisectors are special cases of cevians. The name "cevian" comes from the Italian mathematician Giovanni Ceva, who proved a well-known theorem about cevians which also bears his name.
Quadrature of the Parabola is a treatise on geometry, written by Archimedes in the 3rd century BC and addressed to his Alexandrian acquaintance Dositheus. It contains 24 propositions regarding parabolas, culminating in two proofs showing that the area of a parabolic segment is that of a certain inscribed triangle.
An integer triangle or integral triangle is a triangle all of whose side lengths are integers. A rational triangle is one whose side lengths are rational numbers; any rational triangle can be rescaled by the lowest common denominator of the sides to obtain a similar integer triangle, so there is a close relationship between integer triangles and rational triangles.
