In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and mentioned by German mathematician Georg Cantor in 1883.
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field whose value at a point gives the direction and the rate of fastest increase. The gradient transforms like a vector under change of basis of the space of variables of . If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to minimize a function by gradient descent. In coordinate-free terms, the gradient of a function may be defined by:
Rhythm generally means a "movement marked by the regulated succession of strong and weak elements, or of opposite or different conditions". This general meaning of regular recurrence or pattern in time can apply to a wide variety of cyclical natural phenomena having a periodicity or frequency of anything from microseconds to several seconds ; to several minutes or hours, or, at the most extreme, even over many years.
A time signature is a convention in Western music notation that specifies how many note values of a particular type are contained in each measure (bar). The time signature indicates the meter of a musical movement at the bar level.
In music, metre or meter refers to regularly recurring patterns and accents such as bars and beats. Unlike rhythm, metric onsets are not necessarily sounded, but are nevertheless implied by the performer and expected by the listener.
In mathematical analysis, Hölder's inequality, named after Otto Hölder, is a fundamental inequality between integrals and an indispensable tool for the study of Lp spaces.
In physics, especially in multilinear algebra and tensor analysis, covariance and contravariance describe how the quantitative description of certain geometric or physical entities changes with a change of basis. Briefly, a contravariant vector is a list of numbers that transforms oppositely to a change of basis, and a covariant vector is a list of numbers that transforms in the same way. Contravariant vectors are often just called vectors and covariant vectors are called covectors or dual vectors. The terms covariant and contravariant were introduced by James Joseph Sylvester in 1851.
In music and music theory, the beat is the basic unit of time, the pulse, of the mensural level. The beat is often defined as the rhythm listeners would tap their toes to when listening to a piece of music, or the numbers a musician counts while performing, though in practice this may be technically incorrect. In popular use, beat can refer to a variety of related concepts, including pulse, tempo, meter, specific rhythms, and groove.
In music, a tuplet is "any rhythm that involves dividing the beat into a different number of equal subdivisions from that usually permitted by the time-signature " This is indicated by a number, or sometimes two indicating the fraction involved. The notes involved are also often grouped with a bracket or a slur.
In Western musical notation, a dotted note is a note with a small dot written after it. In modern practice, the first dot increases the duration of the basic note by half of its original value. This means that a dotted note is equivalent to writing the basic note tied to a note of half the value – for instance, a dotted half note is equivalent to a half note tied to a quarter note. Subsequent dots add progressively halved value, as shown in the example to the right.
Amongst the lay public of non-mathematicians and non-scientists, trigonometry is known chiefly for its application to measurement problems, yet is also often used in ways that are far more subtle, such as its place in the theory of music; still other uses are more technical, such as in number theory. The mathematical topics of Fourier series and Fourier transforms rely heavily on knowledge of trigonometric functions and find application in a number of areas, including statistics.
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distances to be measured on that surface. In differential geometry, an affine connection can be defined without reference to a metric, and many additional concepts follow: parallel transport, covariant derivatives, geodesics, etc. also do not require the concept of a metric. However, when a metric is available, these concepts can be directly tied to the "shape" of the manifold itself; that shape is determined by how the tangent space is attached to the cotangent space by the metric tensor. Abstractly, one would say that the manifold has an associated (orthonormal) frame bundle, with each "frame" being a possible choice of a coordinate frame. An invariant metric implies that the structure group of the frame bundle is the orthogonal group O(p, q). As a result, such a manifold is necessarily a (pseudo-)Riemannian manifold. The Christoffel symbols provide a concrete representation of the connection of (pseudo-)Riemannian geometry in terms of coordinates on the manifold. Additional concepts, such as parallel transport, geodesics, etc. can then be expressed in terms of Christoffel symbols.
In mathematics, Hilbert's fourth problem in the 1900 list of Hilbert's problems is a foundational question in geometry. In one statement derived from the original, it was to find — up to an isomorphism — all geometries that have an axiomatic system of the classical geometry, with those axioms of congruence that involve the concept of the angle dropped, and `triangle inequality', regarded as an axiom, added.
In statistics and information theory, a maximum entropy probability distribution has entropy that is at least as great as that of all other members of a specified class of probability distributions. According to the principle of maximum entropy, if nothing is known about a distribution except that it belongs to a certain class, then the distribution with the largest entropy should be chosen as the least-informative default. The motivation is twofold: first, maximizing entropy minimizes the amount of prior information built into the distribution; second, many physical systems tend to move towards maximal entropy configurations over time.
In mathematics, the inverse hyperbolic functions are inverses of the hyperbolic functions, analogous to the inverse circular functions. There are six in common use: inverse hyperbolic sine, inverse hyperbolic cosine, inverse hyperbolic tangent, inverse hyperbolic cosecant, inverse hyperbolic secant, and inverse hyperbolic cotangent. They are commonly denoted by the symbols for the hyperbolic functions, prefixed with arc- or ar-.
In popular music, half-time is a type of meter and tempo that alters the rhythmic feel by essentially doubling the tempo resolution or metric division/level in comparison to common-time. Thus, two measures of 4
4 approximate a single measure of 8
8, while a single measure of 4/4 emulates 2/2. Half-time is not to be confused with alla breve or odd time. Though notes usually get the same value relative to the tempo, the way the beats are divided is altered. While much music typically has a backbeat on quarter note (crotchet) beats two and four, half time would increase the interval between backbeats to double, thus making it hit on beats three and seven, or the third beat of each measure :
1 2 3 4 1 2 3 4 1 2 3 4 5 6 7 8 1 2 3 4
In mathematics, a Madhava series is one of the three Taylor series expansions for the sine, cosine, and arctangent functions discovered in 14th or 15th century in Kerala, India by the mathematician and astronomer Madhava of Sangamagrama or his followers in the Kerala school of astronomy and mathematics. Using modern notation, these series are:
In statistics and in probability theory, distance correlation or distance covariance is a measure of dependence between two paired random vectors of arbitrary, not necessarily equal, dimension. The population distance correlation coefficient is zero if and only if the random vectors are independent. Thus, distance correlation measures both linear and nonlinear association between two random variables or random vectors. This is in contrast to Pearson's correlation, which can only detect linear association between two random variables.
The spectrum of a chirp pulse describes its characteristics in terms of its frequency components. This frequency-domain representation is an alternative to the more familiar time-domain waveform, and the two versions are mathematically related by the Fourier transform. The spectrum is of particular interest when pulses are subject to signal processing. For example, when a chirp pulse is compressed by its matched filter, the resulting waveform contains not only a main narrow pulse but, also, a variety of unwanted artifacts many of which are directly attributable to features in the chirp's spectral characteristics.
= 
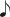), in a piece by J.S. Bach. Slow introduction followed by an allegro traditionally taken at double the speed. Sixteenth notes in the old tempo prepare for eighth notes in the new tempo. 
