
The travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized.

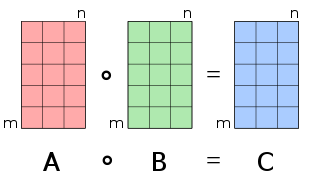
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the second matrix. The resulting matrix, known as the matrix product, has the number of rows of the first and the number of columns of the second matrix. The product of matrices A and B is denoted as AB.

Dynamic programming is both a mathematical optimization method and an algorithmic paradigm. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.
In computer science, the Floyd–Warshall algorithm is an algorithm for finding shortest paths in a directed weighted graph with positive or negative edge weights. A single execution of the algorithm will find the lengths of shortest paths between all pairs of vertices. Although it does not return details of the paths themselves, it is possible to reconstruct the paths with simple modifications to the algorithm. Versions of the algorithm can also be used for finding the transitive closure of a relation , or widest paths between all pairs of vertices in a weighted graph.

In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra. In common geometrical contexts, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector—without changing its direction. The term "scalar" itself derives from this usage: a scalar is that which scales vectors. Scalar multiplication is the multiplication of a vector by a scalar, and is to be distinguished from inner product of two vectors.
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
In mathematics, the Kronecker product, sometimes denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a specialization of the tensor product from vectors to matrices and gives the matrix of the tensor product linear map with respect to a standard choice of basis. The Kronecker product is to be distinguished from the usual matrix multiplication, which is an entirely different operation. The Kronecker product is also sometimes called matrix direct product.
In linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm for matrix multiplication. It is faster than the standard matrix multiplication algorithm for large matrices, with a better asymptotic complexity, although the naive algorithm is often better for smaller matrices. The Strassen algorithm is slower than the fastest known algorithms for extremely large matrices, but such galactic algorithms are not useful in practice, as they are much slower for matrices of practical size. For small matrices even faster algorithms exist.
In mathematics, computer science and especially graph theory, a distance matrix is a square matrix containing the distances, taken pairwise, between the elements of a set. Depending upon the application involved, the distance being used to define this matrix may or may not be a metric. If there are N elements, this matrix will have size N×N. In graph-theoretic applications, the elements are more often referred to as points, nodes or vertices.

In graph theory and network analysis, indicators of centrality assign numbers or rankings to nodes within a graph corresponding to their network position. Applications include identifying the most influential person(s) in a social network, key infrastructure nodes in the Internet or urban networks, super-spreaders of disease, and brain networks. Centrality concepts were first developed in social network analysis, and many of the terms used to measure centrality reflect their sociological origin.
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices.
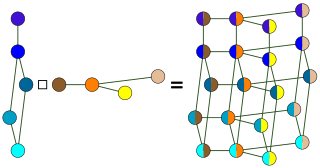
In graph theory, the Cartesian productG □ H of graphs G and H is a graph such that:
A logical matrix, binary matrix, relation matrix, Boolean matrix, or (0, 1)-matrix is a matrix with entries from the Boolean domain B = {0, 1}. Such a matrix can be used to represent a binary relation between a pair of finite sets. It is an important tool in combinatorial mathematics and theoretical computer science.
In chemical graph theory, the Wiener index introduced by Harry Wiener, is a topological index of a molecule, defined as the sum of the lengths of the shortest paths between all pairs of vertices in the chemical graph representing the non-hydrogen atoms in the molecule.

In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns, which is used to represent a mathematical object or a property of such an object.
Because matrix multiplication is such a central operation in many numerical algorithms, much work has been invested in making matrix multiplication algorithms efficient. Applications of matrix multiplication in computational problems are found in many fields including scientific computing and pattern recognition and in seemingly unrelated problems such as counting the paths through a graph. Many different algorithms have been designed for multiplying matrices on different types of hardware, including parallel and distributed systems, where the computational work is spread over multiple processors.
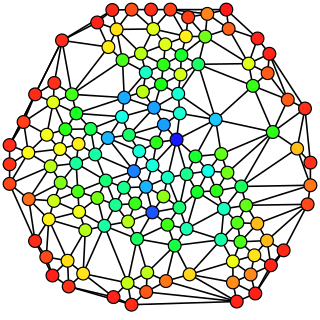
In graph theory, betweenness centrality is a measure of centrality in a graph based on shortest paths. For every pair of vertices in a connected graph, there exists at least one shortest path between the vertices such that either the number of edges that the path passes through or the sum of the weights of the edges is minimized. The betweenness centrality for each vertex is the number of these shortest paths that pass through the vertex.
In mathematics, the Hadamard product is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French-Jewish mathematician Jacques Hadamard or German-Jewish mathematician Issai Schur.
A central problem in algorithmic graph theory is the shortest path problem. Hereby, the problem of finding the shortest path between every pair of nodes is known as all-pair-shortest-paths (APSP) problem. As sequential algorithms for this problem often yield long runtimes, parallelization has shown to be beneficial in this field. In this article two efficient algorithms solving this problem are introduced.


















