In logic and computer science, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation that satisfies a given Boolean formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called satisfiable. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE for all possible variable assignments and the formula is unsatisfiable. For example, the formula "a AND NOT b" is satisfiable because one can find the values a = TRUE and b = FALSE, which make (a AND NOT b) = TRUE. In contrast, "a AND NOT a" is unsatisfiable.
In logic and proof theory, natural deduction is a kind of proof calculus in which logical reasoning is expressed by inference rules closely related to the "natural" way of reasoning. This contrasts with Hilbert-style systems, which instead use axioms as much as possible to express the logical laws of deductive reasoning.
Inductive logic programming (ILP) is a subfield of symbolic artificial intelligence which uses logic programming as a uniform representation for examples, background knowledge and hypotheses. The term "inductive" here refers to philosophical rather than mathematical induction. Given an encoding of the known background knowledge and a set of examples represented as a logical database of facts, an ILP system will derive a hypothesised logic program which entails all the positive and none of the negative examples.
In Boolean logic, a formula is in conjunctive normal form (CNF) or clausal normal form if it is a conjunction of one or more clauses, where a clause is a disjunction of literals; otherwise put, it is a product of sums or an AND of ORs. As a canonical normal form, it is useful in automated theorem proving and circuit theory.
Proof theory is a major branch of mathematical logic and theoretical computer science within which proofs are treated as formal mathematical objects, facilitating their analysis by mathematical techniques. Proofs are typically presented as inductively-defined data structures such as lists, boxed lists, or trees, which are constructed according to the axioms and rules of inference of a given logical system. Consequently, proof theory is syntactic in nature, in contrast to model theory, which is semantic in nature.
In mathematical logic, sequent calculus is a style of formal logical argumentation in which every line of a proof is a conditional tautology instead of an unconditional tautology. Each conditional tautology is inferred from other conditional tautologies on earlier lines in a formal argument according to rules and procedures of inference, giving a better approximation to the natural style of deduction used by mathematicians than to David Hilbert's earlier style of formal logic, in which every line was an unconditional tautology. More subtle distinctions may exist; for example, propositions may implicitly depend upon non-logical axioms. In that case, sequents signify conditional theorems in a first-order language rather than conditional tautologies.
In programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and mathematical proofs.
Modal logic is a kind of logic used to represent statements about necessity and possibility. It plays a major role in philosophy and related fields as a tool for understanding concepts such as knowledge, obligation, and causation. For instance, in epistemic modal logic, the formula can be used to represent the statement that is known. In deontic modal logic, that same formula can represent that is a moral obligation.
In mathematical logic and logic programming, a Horn clause is a logical formula of a particular rule-like form that gives it useful properties for use in logic programming, formal specification, universal algebra and model theory. Horn clauses are named for the logician Alfred Horn, who first pointed out their significance in 1951.
Bunched logic is a variety of substructural logic proposed by Peter O'Hearn and David Pym. Bunched logic provides primitives for reasoning about resource composition, which aid in the compositional analysis of computer and other systems. It has category-theoretic and truth-functional semantics, which can be understood in terms of an abstract concept of resource, and a proof theory in which the contexts Γ in an entailment judgement Γ ⊢ A are tree-like structures (bunches) rather than lists or (multi)sets as in most proof calculi. Bunched logic has an associated type theory, and its first application was in providing a way to control the aliasing and other forms of interference in imperative programs. The logic has seen further applications in program verification, where it is the basis of the assertion language of separation logic, and in systems modelling, where it provides a way to decompose the resources used by components of a system.

In proof theory, the semantic tableau (; plural: tableaux, also called an analytic tableau, truth tree, or simply tree, is a decision procedure for sentential and related logics, and a proof procedure for formulae of first-order logic. An analytic tableau is a tree structure computed for a logical formula, having at each node a subformula of the original formula to be proved or refuted. Computation constructs this tree and uses it to prove or refute the whole formula. The tableau method can also determine the satisfiability of finite sets of formulas of various logics. It is the most popular proof procedure for modal logics.
In formal logic, Horn-satisfiability, or HORNSAT, is the problem of deciding whether a given set of propositional Horn clauses is satisfiable or not. Horn-satisfiability and Horn clauses are named after Alfred Horn.
The closed-world assumption (CWA), in a formal system of logic used for knowledge representation, is the presumption that a statement that is true is also known to be true. Therefore, conversely, what is not currently known to be true, is false. The same name also refers to a logical formalization of this assumption by Raymond Reiter. The opposite of the closed-world assumption is the open-world assumption (OWA), stating that lack of knowledge does not imply falsity. Decisions on CWA vs. OWA determine the understanding of the actual semantics of a conceptual expression with the same notations of concepts. A successful formalization of natural language semantics usually cannot avoid an explicit revelation of whether the implicit logical backgrounds are based on CWA or OWA.
In mathematical logic and automated theorem proving, resolution is a rule of inference leading to a refutation-complete theorem-proving technique for sentences in propositional logic and first-order logic. For propositional logic, systematically applying the resolution rule acts as a decision procedure for formula unsatisfiability, solving the Boolean satisfiability problem. For first-order logic, resolution can be used as the basis for a semi-algorithm for the unsatisfiability problem of first-order logic, providing a more practical method than one following from Gödel's completeness theorem.
Unit propagation (UP) or Boolean Constraint propagation (BCP) or the one-literal rule (OLR) is a procedure of automated theorem proving that can simplify a set of clauses.
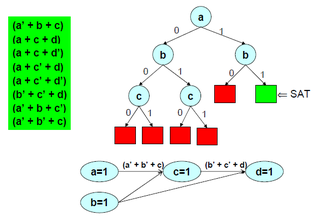
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.
In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involving real numbers, integers, and/or various data structures such as lists, arrays, bit vectors, and strings. The name is derived from the fact that these expressions are interpreted within ("modulo") a certain formal theory in first-order logic with equality. SMT solvers are tools that aim to solve the SMT problem for a practical subset of inputs. SMT solvers such as Z3 and cvc5 have been used as a building block for a wide range of applications across computer science, including in automated theorem proving, program analysis, program verification, and software testing.
In mathematical logic, the hypersequent framework is an extension of the proof-theoretical framework of sequent calculi used in structural proof theory to provide analytic calculi for logics that are not captured in the sequent framework. A hypersequent is usually taken to be a finite multiset of ordinary sequents, written
A non-normal modal logic is a variant of modal logic that deviates from the basic principles of normal modal logics.
Counterexample-guided abstraction refinement (CEGAR) is a technique for symbolic model checking. It is also applied in modal logic tableau calculi algorithms to optimise their efficiency.







