Identity and generalisation
It is a special case of the more general identity
with n = 3 and α = 20° and the fact that
since
Morrie's law is a special trigonometric identity. Its name is due to the physicist Richard Feynman, who used to refer to the identity under that name. Feynman picked that name because he learned it during his childhood from a boy with the name Morrie Jacobs and afterwards remembered it for all of his life. [1]
It is a special case of the more general identity
with n = 3 and α = 20° and the fact that
since
A similar identity for the sine function also holds:
Moreover, dividing the second identity by the first, the following identity is evident:
![Regular nonagon
A
B
C
D
E
F
G
H
I
{\displaystyle ABCDEFGHI}
with
O
{\displaystyle O}
being the center of its circumcircle. Computing of the angles:
40
[?]
=
360
[?]
9
70
[?]
=
180
[?]
-
40
[?]
2
a
=
180
[?]
-
90
[?]
-
70
[?]
=
20
[?]
b
=
180
[?]
-
90
[?]
-
(
70
[?]
-
a
)
=
40
[?]
g
=
140
[?]
-
b
-
a
=
80
[?]
{\displaystyle {\begin{aligned}40^{\circ }&={\frac {360^{\circ }}{9}}\\70^{\circ }&={\frac {180^{\circ }-40^{\circ }}{2}}\\\alpha &=180^{\circ }-90^{\circ }-70^{\circ }=20^{\circ }\\\beta &=180^{\circ }-90^{\circ }-(70^{\circ }-\alpha )=40^{\circ }\\\gamma &=140^{\circ }-\beta -\alpha =80^{\circ }\end{aligned}}} Morries law geometric proof.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/5/5a/Morries_law_geometric_proof.svg/330px-Morries_law_geometric_proof.svg.png)
Consider a regular nonagon with side length and let be the midpoint of , the midpoint and the midpoint of . The inner angles of the nonagon equal and furthermore , and (see graphic). Applying the cosinus definition in the right angle triangles , and then yields the proof for Morrie's law: [2]
Recall the double angle formula for the sine function
Solve for
It follows that:
Multiplying all of these expressions together yields:
The intermediate numerators and denominators cancel leaving only the first denominator, a power of 2 and the final numerator. Note that there are n terms in both sides of the expression. Thus,
which is equivalent to the generalization of Morrie's law.

In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square.

In mathematical physics and mathematics, the Pauli matrices are a set of three 2 × 2 complex matrices that are traceless, Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma, they are occasionally denoted by tau when used in connection with isospin symmetries.

A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.

In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law, where a, b, and c are the lengths of the sides of a triangle, and α, β, and γ are the opposite angles, while R is the radius of the triangle's circumcircle. When the last part of the equation is not used, the law is sometimes stated using the reciprocals; The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the triangle is not uniquely determined by this data and the technique gives two possible values for the enclosed angle.
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space under the operation of composition.
Unit quaternions, known as versors, provide a convenient mathematical notation for representing spatial orientations and rotations of elements in three dimensional space. Specifically, they encode information about an axis-angle rotation about an arbitrary axis. Rotation and orientation quaternions have applications in computer graphics, computer vision, robotics, navigation, molecular dynamics, flight dynamics, orbital mechanics of satellites, and crystallographic texture analysis.

In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral

In plane geometry, Morley's trisector theorem states that in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle, called the first Morley triangle or simply the Morley triangle. The theorem was discovered in 1899 by Anglo-American mathematician Frank Morley. It has various generalizations; in particular, if all the trisectors are intersected, one obtains four other equilateral triangles.
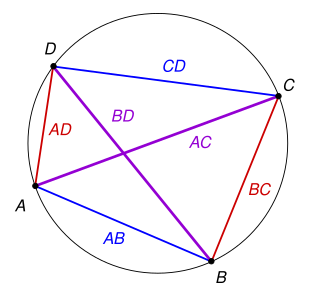
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral. The theorem is named after the Greek astronomer and mathematician Ptolemy. Ptolemy used the theorem as an aid to creating his table of chords, a trigonometric table that he applied to astronomy.

In geometry, Bretschneider's formula is a mathematical expression for the area of a general quadrilateral. It works on both convex and concave quadrilaterals, whether it is cyclic or not.
In geometry, various formalisms exist to express a rotation in three dimensions as a mathematical transformation. In physics, this concept is applied to classical mechanics where rotational kinematics is the science of quantitative description of a purely rotational motion. The orientation of an object at a given instant is described with the same tools, as it is defined as an imaginary rotation from a reference placement in space, rather than an actually observed rotation from a previous placement in space.
The Wigner D-matrix is a unitary matrix in an irreducible representation of the groups SU(2) and SO(3). It was introduced in 1927 by Eugene Wigner, and plays a fundamental role in the quantum mechanical theory of angular momentum. The complex conjugate of the D-matrix is an eigenfunction of the Hamiltonian of spherical and symmetric rigid rotors. The letter D stands for Darstellung, which means "representation" in German.

A biarc is a smooth curve formed from two circular arcs. In order to make the biarc smooth, the two arcs should have the same tangent at the connecting point where they meet.

In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. For a triangle with sides and opposite respective angles and , the law of cosines states:
In hyperbolic geometry, the "law of cosines" is a pair of theorems relating the sides and angles of triangles on a hyperbolic plane, analogous to the planar law of cosines from plane trigonometry, or the spherical law of cosines in spherical trigonometry. It can also be related to the relativistic velocity addition formula.

In trigonometry, Mollweide's formula is a pair of relationships between sides and angles in a triangle.
Solution of triangles is the main trigonometric problem of finding the characteristics of a triangle, when some of these are known. The triangle can be located on a plane or on a sphere. Applications requiring triangle solutions include geodesy, astronomy, construction, and navigation.
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.
In mathematics, infinite compositions of analytic functions (ICAF) offer alternative formulations of analytic continued fractions, series, products and other infinite expansions, and the theory evolving from such compositions may shed light on the convergence/divergence of these expansions. Some functions can actually be expanded directly as infinite compositions. In addition, it is possible to use ICAF to evaluate solutions of fixed point equations involving infinite expansions. Complex dynamics offers another venue for iteration of systems of functions rather than a single function. For infinite compositions of a single function see Iterated function. For compositions of a finite number of functions, useful in fractal theory, see Iterated function system.