Multi-swarm optimization

Last updated

Multi-swarm optimization is a variant of particle swarm optimization (PSO) based on the use of multiple sub-swarms instead of one (standard) swarm. The general approach in multi-swarm optimization is that each sub-swarm focuses on a specific region while a specific diversification method decides where and when to launch the sub-swarms. The multi-swarm framework is especially fitted for the optimization on multi-modal problems, where multiple (local) optima exist.

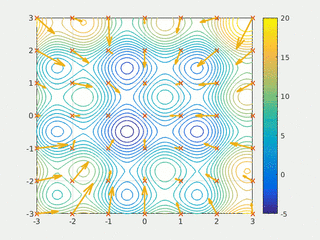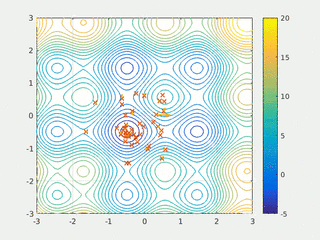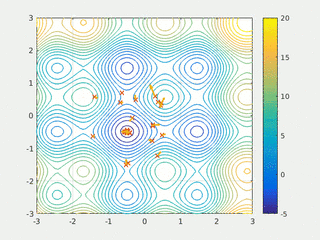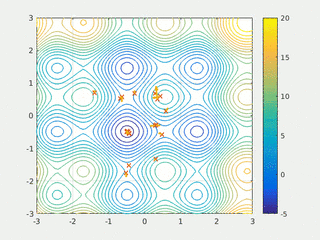
Particle swarm optimization Iterative simulation method

In computational science, particle swarm optimization (PSO) is a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. It solves a problem by having a population of candidate solutions, here dubbed particles, and moving these particles around in the search-space according to simple mathematical formulae over the particle's position and velocity. Each particle's movement is influenced by its local best known position, but is also guided toward the best known positions in the search-space, which are updated as better positions are found by other particles. This is expected to move the swarm toward the best solutions.

Contents

Description

In multi-modal problems it is important to achieve an effective balance between exploration and exploitation. Multi-swarm systems provide a new approach to improve this balance. Instead of trying to achieve a compromise between exploration and exploitation which could weaken both mechanisms of the search process, multi-swarm systems separate them into distinct phases. Each phase is more focused on either exploitation (individual sub-swarms) or exploration (diversification method).

The coordination of the sub-swarms depends on the specific diversification method(s) implemented by the multi-swarm system. Wave of Swarm of Particles (WOSP), [1] for example, bases its diversification mechanism on the "collision" of particles. When particles get too close they are expelled by a short range force into new waves/sub-swarms, avoiding thus a complete convergence. The Dynamic Multi-Swarm-Particle Swarm Optimizer (DMS-PSO) [2] periodically regroups the particles of the sub-swarms (after they have converged) into new sub-swarms, the new swarms are started with particles from previous swarms. Locust swarms [3] are based on a "devour and move on" strategy – after a sub-swarm "devours" a relatively small region of the search space (to find a local optimum) scouts are deployed to look for new promising regions to "move on".

A distinctive feature of sub-swarms is that their initial positions and initial velocities are not randomly selected as in normal swarms. Instead, they maintain some information from the previous trajectories of the particles. In general, the development of multi-swarm systems leads to design decisions which did not exist during the original development of particle swarm optimization, such as the number of particles to use in each sub-swarm, the optimal value for the constriction factor and the effects of non-random initial positions and initial velocities. These design decisions have been thoroughly studied and have well-established guidelines – e.g. the use of non-random initial positions and initial velocities leads to improved results in multi-swarm systems, which is not the case for single-swarms. [4] Other design decisions, such as which diversification method to use or which specific search strategy will select the initial positions and initial velocities of a sub-swarm, have less established guidelines and constitute open questions in the field of multi-swarm systems.

Some of these design decisions can be addressed by relatively independent sub-components which allow different optimization techniques to be inserted. Multi-swarm systems thus provide a useful framework for the development of hybrid algorithms. For example, the UMDA-PSO [5] multi-swarm system effectively combines components from particle swarm optimization, estimation of distribution algorithm, and differential evolution into a multi-swarm hybrid.

A hybrid algorithm is an algorithm that combines two or more other algorithms that solve the same problem, either choosing one, or switching between them over the course of the algorithm. This is generally done to combine desired features of each, so that the overall algorithm is better than the individual components.

Estimation of distribution algorithm

Estimation of distribution algorithms (EDAs), sometimes called probabilistic model-building genetic algorithms (PMBGAs), are stochastic optimization methods that guide the search for the optimum by building and sampling explicit probabilistic models of promising candidate solutions. Optimization is viewed as a series of incremental updates of a probabilistic model, starting with the model encoding an uninformative prior over admissible solutions and ending with the model that generates only the global optima.

Differential evolution

In evolutionary computation, differential evolution (DE) is a method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Such methods are commonly known as metaheuristics as they make few or no assumptions about the problem being optimized and can search very large spaces of candidate solutions. However, metaheuristics such as DE do not guarantee an optimal solution is ever found.

Current work

A reading group on Mendeley is available to all interested researchers.

Mendeley social reference management software

Mendeley is a desktop and web program produced by Elsevier for managing and sharing research papers, discovering research data and collaborating online. It combines Mendeley Desktop, a PDF and reference management application available for Windows, macOS and Linux. It also provides Mendeley for Android and iOS, with Mendeley Web, an online social network for researchers.

See also

Related Research Articles

Genetic algorithm competitive algorithm for searching a problem space

In computer science and operations research, a genetic algorithm (GA) is a metaheuristic inspired by the process of natural selection that belongs to the larger class of evolutionary algorithms (EA). Genetic algorithms are commonly used to generate high-quality solutions to optimization and search problems by relying on bio-inspired operators such as mutation, crossover and selection. John Holland introduced genetic algorithms in 1960 based on the concept of Darwin’s theory of evolution; afterwards, his student David E. Goldberg extended GA in 1989.

In artificial intelligence, an evolutionary algorithm (EA) is a subset of evolutionary computation, a generic population-based metaheuristic optimization algorithm. An EA uses mechanisms inspired by biological evolution, such as reproduction, mutation, recombination, and selection. Candidate solutions to the optimization problem play the role of individuals in a population, and the fitness function determines the quality of the solutions. Evolution of the population then takes place after the repeated application of the above operators.

Ant colony optimization algorithms

In computer science and operations research, the ant colony optimization algorithm (ACO) is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. Artificial Ants stand for multi-agent methods inspired by the behavior of real ants. The pheromone-based communication of biological ants is often the predominant paradigm used. Combinations of Artificial Ants and local search algorithms have become a method of choice for numerous optimization tasks involving some sort of graph, e.g., vehicle routing and internet routing. The burgeoning activity in this field has led to conferences dedicated solely to Artificial Ants, and to numerous commercial applications by specialized companies such as AntOptima.

Swarm intelligence (SI) is the collective behavior of decentralized, self-organized systems, natural or artificial. The concept is employed in work on artificial intelligence. The expression was introduced by Gerardo Beni and Jing Wang in 1989, in the context of cellular robotic systems.

In computer science and mathematical optimization, a metaheuristic is a higher-level procedure or heuristic designed to find, generate, or select a heuristic that may provide a sufficiently good solution to an optimization problem, especially with incomplete or imperfect information or limited computation capacity. Metaheuristics sample a set of solutions which is too large to be completely sampled. Metaheuristics may make few assumptions about the optimization problem being solved, and so they may be usable for a variety of problems.

In computer science and operations research, a memetic algorithm (MA) is an extension of the traditional genetic algorithm. It uses a local search technique to reduce the likelihood of the premature convergence.

Multi-objective optimization is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives.

Cultural algorithms (CA) are a branch of evolutionary computation where there is a knowledge component that is called the belief space in addition to the population component. In this sense, cultural algorithms can be seen as an extension to a conventional genetic algorithm. Cultural algorithms were introduced by Reynolds.

ParadisEO is a white-box object-oriented framework dedicated to the flexible design of metaheuristics. It uses EO, a template-based, ANSI-C++ compliant computation library. ParadisEO is portable across both Windows system and sequential platforms. ParadisEO is distributed under the CeCill license and can be used under several environments.

Parallel metaheuristic is a class of techniques that are capable of reducing both the numerical effort and the run time of a metaheuristic. To this end, concepts and technologies from the field of parallelism in computer science are used to enhance and even completely modify the behavior of existing metaheuristics. Just as it exists a long list of metaheuristics like evolutionary algorithms, particle swarm, ant colony optimization, simulated annealing, etc. it also exists a large set of different techniques strongly or loosely based in these ones, whose behavior encompasses the multiple parallel execution of algorithm components that cooperate in some way to solve a problem on a given parallel hardware platform.

Design Automation usually refers to electronic design automation, or Design Automation which is a Product Configurator. Extending Computer-Aided Design (CAD), automated design and Computer-Automated Design (CAutoD) are more concerned with a broader range of applications, such as automotive engineering, civil engineering, composite material design, control engineering, dynamic system identification and optimization, financial systems, industrial equipment, mechatronic systems, steel construction, structural optimisation, and the invention of novel systems.

Meta-optimization

In numerical optimization, meta-optimization is the use of one optimization method to tune another optimization method. Meta-optimization is reported to have been used as early as in the late 1970s by Mercer and Sampson for finding optimal parameter settings of a genetic algorithm.

In applied mathematics, multimodal optimization deals with optimization tasks that involve finding all or most of the multiple solutions of a problem, as opposed to a single best solution. Evolutionary multimodal optimization is a branch of evolutionary computation, which is closely related to machine learning. Wong provides a short survey, wherein the chapter of Shir and the book of Preuss cover the topic in more detail.

In computer science, imperialist competitive algorithm is a computational method that is used to solve optimization problems of different types. Like most of the methods in the area of evolutionary computation, ICA does not need the gradient of the function in its optimization process. From a specific point of view, ICA can be thought of as the social counterpart of genetic algorithms (GAs). ICA is the mathematical model and the computer simulation of human social evolution, while GAs are based on the biological evolution of species.

The constructive cooperative coevolutionary algorithm (also called C3) is a global optimisation algorithm in artificial intelligence based on the multi-start architecture of the greedy randomized adaptive search procedure (GRASP). It incorporates the existing cooperative coevolutionary algorithm (CC). The considered problem is decomposed into subproblems. These subproblems are optimised separately while exchanging information in order to solve the complete problem. An optimisation algorithm, usually but not necessarily an evolutionary algorithm, is embedded in C3 for optimising those subproblems. The nature of the embedded optimisation algorithm determines whether C3's behaviour is deterministic or stochastic.

The Genetic and Evolutionary Computation Conference (GECCO) is the premier conference in the area of genetic and evolutionary computation. GECCO has been held every year since 1999, when it was first established as a recombination of the International Conference on Genetic Algorithms (ICGA) and the Annual Genetic Programming Conference (GP).

Fish School Search (FSS), proposed by Bastos Filho and Lima Neto in 2007 is, in its basic version, an unimodal optimization algorithm inspired on the collective behavior of fish schools. The mechanisms of feeding and coordinated movement were used as inspiration to create the search operators. The core idea is to make the fishes “swim” toward the positive gradient in order to “eat” and “gain weight”. Collectively, the heavier fishes are more influent in the search process as a whole, what makes the barycenter of the fish school moves toward better places in the search space over the iterations.

References

  1. ↑ T. Hendtlass, "WoSP: A Multi-Optima Particle Swarm Algorithm," in Proceedings IEEE Congress on Evolutionary Computation, 2005, pp. 727–734.
  2. ↑ S. Z. Zhao, J. J. Liang, P. N. Suganthan, and M. F. Tasgetiren, "Dynamic Multi-Swarm Particle Swarm Optimizer with Local Search for Large Scale Global Optimization," in Proceedings IEEE Congress on Evolutionary Computation, 2008, pp. 3845–3852.
  3. ↑ S. Chen, "Locust Swarms – A New Multi-Optima Search Technique", in Proceedings of the IEEE Congress on Evolutionary Computation, 2009, pp. 1745–1752.
  4. ↑ S.Chen and J. Montgomery "Selection Strategies for Initial Positions and Initial Velocities in Multi–optima Particle Swarms", in Proceedings of the Genetic and Evolutionary Computation Conference, 2011 pp. 53–60.
  5. ↑ Antonio Bolufé Röhler and S. Chen, "Multi-swarm hybrid for multi-modal optimization", in Proceedings of the IEEE Congress on Evolutionary Computation, 2012, pp. 1759-1766.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.