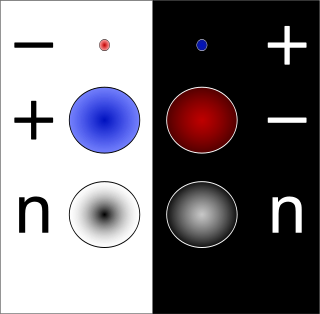
In particle physics, every type of particle is associated with an antiparticle with the same mass but with opposite physical charges. For example, the antiparticle of the electron is the positron. While the electron has a negative electric charge, the positron has a positive electric charge, and is produced naturally in certain types of radioactive decay. The opposite is also true: the antiparticle of the positron is the electron.

In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after early 19th century mathematician Niels Henrik Abel.

In mathematics, a group is a set and an operation that combines any two elements of the set to produce a third element of the set, in such a way that the operation is associative, an identity element exists and every element has an inverse. These three axioms hold for number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it was elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics.

In theoretical physics, quantum field theory (QFT) is a theoretical framework that combines classical field theory, special relativity, and quantum mechanics. QFT is used in particle physics to construct physical models of subatomic particles and in condensed matter physics to construct models of quasiparticles.

In nuclear physics and particle physics, the weak interaction, which is also often called the weak force or weak nuclear force, is one of the four known fundamental interactions, with the others being electromagnetism, the strong interaction, and gravitation. It is the mechanism of interaction between subatomic particles that is responsible for the radioactive decay of atoms: The weak interaction participates in nuclear fission and nuclear fusion. The theory describing its behaviour and effects is sometimes called quantum flavourdynamics (QFD); however, the term QFD is rarely used, because the weak force is better understood by electroweak theory (EWT).

The Standard Model of particle physics is the theory describing three of the four known fundamental forces in the universe and classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists worldwide, with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, proof of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

A gauge theory is a type of theory in physics. The word gauge means a measurement, a thickness, an in-between distance, or a resulting number of units per certain parameter. Modern theories describe physical forces in terms of fields, e.g., the electromagnetic field, the gravitational field, and fields that describe forces between the elementary particles. A general feature of these field theories is that the fundamental fields cannot be directly measured; however, some associated quantities can be measured, such as charges, energies, and velocities. For example, say you cannot measure the diameter of a lead ball, but you can determine how many lead balls, which are equal in every way, are required to make a pound. Using the number of balls, the density of lead, and the formula for calculating the volume of a sphere from its diameter, one could indirectly determine the diameter of a single lead ball. In field theories, different configurations of the unobservable fields can result in identical observable quantities. A transformation from one such field configuration to another is called a gauge transformation; the lack of change in the measurable quantities, despite the field being transformed, is a property called gauge invariance. For example, if you could measure the color of lead balls and discover that when you change the color, you still fit the same number of balls in a pound, the property of "color" would show gauge invariance. Since any kind of invariance under a field transformation is considered a symmetry, gauge invariance is sometimes called gauge symmetry. Generally, any theory that has the property of gauge invariance is considered a gauge theory.
In particle physics, the baryon number is a strictly conserved additive quantum number of a system. It is defined as

In mathematics, the circle group, denoted by or 1, is the multiplicative group of all complex numbers with absolute value 1, that is, the unit circle in the complex plane or simply the unit complex numbers

In quantum physics and chemistry, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.

In mathematics and group theory, the term multiplicative group refers to one of the following concepts:
A chiral phenomenon is one that is not identical to its mirror image. The spin of a particle may be used to define a handedness, or helicity, for that particle, which, in the case of a massless particle, is the same as chirality. A symmetry transformation between the two is called parity transformation. Invariance under parity transformation by a Dirac fermion is called chiral symmetry.
In quantum mechanics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it can also refer to the simultaneous flip in the sign of all three spatial coordinates :
In particle physics, lepton number is a conserved quantum number representing the difference between the number of leptons and the number of antileptons in an elementary particle reaction. Lepton number is an additive quantum number, so its sum is preserved in interactions. Mathematically, the lepton number is defined by
In the Standard Model of electroweak interactions of particle physics, the weak hypercharge is a quantum number relating the electric charge and the third component of weak isospin. It is frequently denoted and corresponds to the gauge symmetry U(1).
In particle physics, flavour or flavor refers to the species of an elementary particle. The Standard Model counts six flavours of quarks and six flavours of leptons. They are conventionally parameterized with flavour quantum numbers that are assigned to all subatomic particles. They can also be described by some of the family symmetries proposed for the quark-lepton generations.

In particle physics, the quark model is a classification scheme for hadrons in terms of their valence quarks—the quarks and antiquarks which give rise to the quantum numbers of the hadrons. The quark model underlies "flavor SU(3)", or the Eightfold Way, the successful classification scheme organizing the large number of lighter hadrons that were being discovered starting in the 1950s and continuing through the 1960s. It received experimental verification beginning in the late 1960s and is a valid effective classification of them to date. The model was independently proposed by physicists Murray Gell-Mann, who dubbed them "quarks" in a concise paper, and George Zweig, who suggested "aces" in a longer manuscript. André Petermann also touched upon the central ideas from 1963 to 1965, without as much quantitative substantiation. Today, the model has essentially been absorbed as a component of the established quantum field theory of strong and electroweak particle interactions, dubbed the Standard Model.

This article describes the mathematics of the Standard Model of particle physics, a gauge quantum field theory containing the internal symmetries of the unitary product group SU(3) × SU(2) × U(1). The theory is commonly viewed as describing the fundamental set of particles – the leptons, quarks, gauge bosons and the Higgs boson.
In physics, a charge is any of many different quantities, such as the electric charge in electromagnetism or the color charge in quantum chromodynamics. Charges correspond to the time-invariant generators of a symmetry group, and specifically, to the generators that commute with the Hamiltonian. Charges are often denoted by the letter Q, and so the invariance of the charge corresponds to the vanishing commutator , where H is the Hamiltonian. Thus, charges are associated with conserved quantum numbers; these are the eigenvalues q of the generator Q.

Symmetries in quantum mechanics describe features of spacetime and particles which are unchanged under some transformation, in the context of quantum mechanics, relativistic quantum mechanics and quantum field theory, and with applications in the mathematical formulation of the standard model and condensed matter physics. In general, symmetry in physics, invariance, and conservation laws, are fundamentally important constraints for formulating physical theories and models. In practice, they are powerful methods for solving problems and predicting what can happen. While conservation laws do not always give the answer to the problem directly, they form the correct constraints and the first steps to solving a multitude of problems.