| Class | Approximation algorithm |
|---|---|
| Data structure | Graph |
| Worst-case performance | |
| Worst-case space complexity | |
| Optimal | No |
The nearest neighbour algorithm was one of the first algorithms used to solve the travelling salesman problem approximately. In that problem, the salesman starts at a random city and repeatedly visits the nearest city until all have been visited. The algorithm quickly yields a short tour, but usually not the optimal one.
These are the steps of the algorithm:
The sequence of the visited vertices is the output of the algorithm.
The nearest neighbour algorithm is easy to implement and executes quickly, but it can sometimes miss shorter routes which are easily noticed with human insight, due to its "greedy" nature. As a general guide, if the last few stages of the tour are comparable in length to the first stages, then the tour is reasonable; if they are much greater, then it is likely that much better tours exist. Another check is to use an algorithm such as the lower bound algorithm to estimate if this tour is good enough.
In the worst case, the algorithm results in a tour that is much longer than the optimal tour. To be precise, for every constant r there is an instance of the traveling salesman problem such that the length of the tour computed by the nearest neighbour algorithm is greater than r times the length of the optimal tour. Moreover, for each number of cities there is an assignment of distances between the cities for which the nearest neighbour heuristic produces the unique worst possible tour. (If the algorithm is applied on every vertex as the starting vertex, the best path found will be better than at least N/2-1 other tours, where N is the number of vertices.) [1]
The nearest neighbour algorithm may not find a feasible tour at all, even when one exists.
In the theory of computational complexity, the travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
Dijkstra's algorithm is an algorithm for finding the shortest paths between nodes in a weighted graph, which may represent, for example, a road network. It was conceived by computer scientist Edsger W. Dijkstra in 1956 and published three years later.
A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
In graph theory and combinatorial optimization, Guan's route problem, the Chinese postman problem, postman tour or route inspection problem is to find a shortest closed path or circuit that visits every edge of an (connected) undirected graph at least once. When the graph has an Eulerian circuit, that circuit is an optimal solution. Otherwise, the optimization problem is to find the smallest number of graph edges to duplicate so that the resulting multigraph does have an Eulerian circuit. It can be solved in polynomial time, unlike the Travelling Salesman Problem which is NP-hard. It is different from the Travelling Salesman Problem in that the travelling salesman cannot repeat visited nodes and does not have to visit every edge.
The Bellman–Ford algorithm is an algorithm that computes shortest paths from a single source vertex to all of the other vertices in a weighted digraph. It is slower than Dijkstra's algorithm for the same problem, but more versatile, as it is capable of handling graphs in which some of the edge weights are negative numbers. The algorithm was first proposed by Alfonso Shimbel, but is instead named after Richard Bellman and Lester Ford Jr., who published it in 1958 and 1956, respectively. Edward F. Moore also published a variation of the algorithm in 1959, and for this reason it is also sometimes called the Bellman–Ford–Moore algorithm.
In computer science, local search is a heuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution that maximizes a criterion among a number of candidate solutions. Local search algorithms move from solution to solution in the space of candidate solutions by applying local changes, until a solution deemed optimal is found or a time bound is elapsed.
The Bottleneck traveling salesman problem is a problem in discrete or combinatorial optimization. The problem is to find the Hamiltonian cycle in a weighted graph which minimizes the weight of the highest-weight edge of the cycle. It was first formulated by Gilmore & Gomory (1964) with some additional constraints, and in its full generality by Garfinkel & Gilbert (1978).
Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are also many approximation algorithms that provide an additive guarantee on the quality of the returned solution. A notable example of an approximation algorithm that provides both is the classic approximation algorithm of Lenstra, Shmoys and Tardos for scheduling on unrelated parallel machines.
In graph theory, a dominating set for a graph G is a subset D of its vertices, such that any vertex of G is in D, or has a neighbor in D. The domination numberγ(G) is the number of vertices in a smallest dominating set for G.
Domination analysis of an approximation algorithm is a way to estimate its performance, introduced by Glover and Punnen in 1997. Unlike the classical approximation ratio analysis, which compares the numerical quality of a calculated solution with that of an optimal solution, domination analysis involves examining the rank of the calculated solution in the sorted order of all possible solutions. In this style of analysis, an algorithm is said to have dominance number or domination numberK, if there exists a subset of K different solutions to the problem among which the algorithm's output is the best. Domination analysis can also be expressed using a domination ratio, which is the fraction of the solution space that is no better than the given solution; this number always lies within the interval [0,1], with larger numbers indicating better solutions. Domination analysis is most commonly applied to problems for which the total number of possible solutions is known and for which exact solution is difficult.
The Christofides algorithm or Christofides–Serdyukov algorithm is an algorithm for finding approximate solutions to the travelling salesman problem, on instances where the distances form a metric space . It is an approximation algorithm that guarantees that its solutions will be within a factor of 3/2 of the optimal solution length, and is named after Nicos Christofides and Anatoliy I. Serdyukov ; the latter discovered it independently in 1976.
In computer science, Kosaraju-Sharir's algorithm is a linear time algorithm to find the strongly connected components of a directed graph. Aho, Hopcroft and Ullman credit it to S. Rao Kosaraju and Micha Sharir. Kosaraju suggested it in 1978 but did not publish it, while Sharir independently discovered it and published it in 1981. It makes use of the fact that the transpose graph has exactly the same strongly connected components as the original graph.
In computer science, graph traversal refers to the process of visiting each vertex in a graph. Such traversals are classified by the order in which the vertices are visited. Tree traversal is a special case of graph traversal.
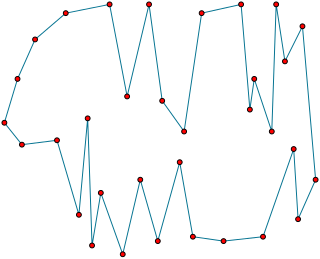
In computational geometry, a bitonic tour of a set of point sites in the Euclidean plane is a closed polygonal chain that has each site as one of its vertices, such that any vertical line crosses the chain at most twice.
In graph theory, a branch of discrete mathematics, a distance-hereditary graph is a graph in which the distances in any connected induced subgraph are the same as they are in the original graph. Thus, any induced subgraph inherits the distances of the larger graph.
In a graph, a maximum cut is a cut whose size is at least the size of any other cut. That is, it is a partition of the graph's vertices into two complementary sets S and T, such that the number of edges between S and T is as large as possible. Finding such a cut is known as the max-cut problem.
In the study of graph coloring problems in mathematics and computer science, a greedy coloring or sequential coloring is a coloring of the vertices of a graph formed by a greedy algorithm that considers the vertices of the graph in sequence and assigns each vertex its first available color. Greedy colorings can be found in linear time, but they do not, in general, use the minimum number of colors possible.
In combinatorial optimization, the set TSP, also known as the generalized TSP, group TSP, One-of-a-Set TSP, Multiple Choice TSP or Covering Salesman Problem, is a generalization of the traveling salesman problem (TSP), whereby it is required to find a shortest tour in a graph which visits all specified subsets of the vertices of a graph. The subsets of vertices must be disjoint, since the case of overlapping subsets can be reduced to the case of disjoint ones. The ordinary TSP is a special case of the set TSP when all subsets to be visited are singletons. Therefore, the set TSP is also NP-hard.
In graph theory, the metric k-center problem or vertex k-center problem is a classical combinatorial optimization problem studied in theoretical computer science that is NP-hard. Given n cities with specified distances, one wants to build k warehouses in different cities and minimize the maximum distance of a city to a warehouse. In graph theory, this means finding a set of k vertices for which the largest distance of any point to its closest vertex in the k-set is minimum. The vertices must be in a metric space, providing a complete graph that satisfies the triangle inequality. It has application in facility location and clustering.
