In mathematics, an elementary function is a function of a single variable that is defined as taking sums, products, and compositions of finitely many polynomial, rational, trigonometric, hyperbolic, and exponential functions, including possibly their inverse functions.
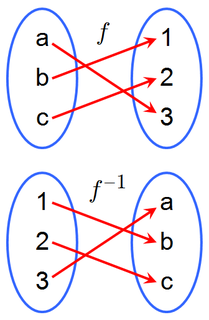
In mathematics, the inverse function of a function f is a function that undoes the operation of f. The inverse of f exists if and only if f is bijective, and if it exists, is denoted by

In mathematics, a group is a set and an operation that combines any two elements of the set to produce a third element of the set, in such a way that the operation is associative, an identity element exists and every element has an inverse. These three axioms hold for number systems and many other mathematical structures. For example, the integers together with the addition operation form a group. The concept of a group and the axioms that define it was elaborated for handling, in a unified way, essential structural properties of very different mathematical entities such as numbers, geometric shapes and polynomial roots. Because the concept of groups is ubiquitous in numerous areas both within and outside mathematics, some authors consider it as a central organizing principle of contemporary mathematics.
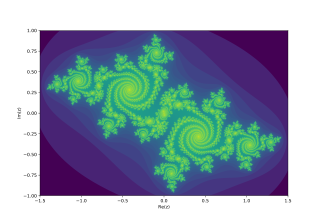
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function. Informally, the Fatou set of the function consists of values with the property that all nearby values behave similarly under repeated iteration of the function, and the Julia set consists of values such that an arbitrarily small perturbation can cause drastic changes in the sequence of iterated function values. Thus the behavior of the function on the Fatou set is "regular", while on the Julia set its behavior is "chaotic".

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of noncommutative rings where multiplication is not required to be commutative.

Exponentiation is a mathematical operation, written as bn, involving two numbers, the baseb and the exponent or powern, and pronounced as "b raised to the power of n". When n is a positive integer, exponentiation corresponds to repeated multiplication of the base: that is, bn is the product of multiplying n bases:

In mathematics, a function from a set X to a set Y assigns to each element of X exactly one element of Y. The set X is called the domain of the function and the set Y is called the codomain of the function.
In mathematics, specifically differential calculus, the inverse function theorem gives a sufficient condition for a function to be invertible in a neighborhood of a point in its domain: namely, that its derivative is continuous and non-zero at the point. The theorem also gives a formula for the derivative of the inverse function. In multivariable calculus, this theorem can be generalized to any continuously differentiable, vector-valued function whose Jacobian determinant is nonzero at a point in its domain, giving a formula for the Jacobian matrix of the inverse. There are also versions of the inverse function theorem for complex holomorphic functions, for differentiable maps between manifolds, for differentiable functions between Banach spaces, and so forth.
The theory of functions of several complex variables is the branch of mathematics dealing with complex-valued functions. The name of the field dealing with the properties of function of several complex variables is called several complex variables, that has become a common name for that whole field of study and Mathematics Subject Classification has, as a top-level heading. A function is n-tuples of complex numbers, classically studied on the complex coordinate space .
In functional analysis, a branch of mathematics, a compact operator is a linear operator , where are normed vector spaces, with the property that maps bounded subsets of to relatively compact subsets of . Such an operator is necessarily a bounded operator, and so continuous. Some authors require that are Banach, but the definition can be extended to more general spaces.
In mathematics, a rational variety is an algebraic variety, over a given field K, which is birationally equivalent to a projective space of some dimension over K. This means that its function field is isomorphic to
In mathematics, particularly in combinatorics, given a family of sets, here called a collection C, a transversal is a set containing exactly one element from each member of the collection. When the sets of the collection are mutually disjoint, each element of the transversal corresponds to exactly one member of C. If the original sets are not disjoint, there are two possibilities for the definition of a transversal:
In mathematics, Carathéodory's theorem is a theorem in complex analysis, named after Constantin Carathéodory, which extends the Riemann mapping theorem. The theorem, first proved in 1913, states that the conformal mapping sending the unit disk to the region in the complex plane bounded by a Jordan curve extends continuously to a homeomorphism from the unit circle onto the Jordan curve. The result is one of Carathéodory's results on prime ends and the boundary behaviour of univalent holomorphic functions.
In mathematics, Fatou components are components of the Fatou set. They were named after Pierre Fatou.
Siegel disc is a connected component in the Fatou set where the dynamics is analytically conjugate to an irrational rotation.
Arithmetic dynamics is a field that amalgamates two areas of mathematics, dynamical systems and number theory. Classically, discrete dynamics refers to the study of the iteration of self-maps of the complex plane or real line. Arithmetic dynamics is the study of the number-theoretic properties of integer, rational, p-adic, and/or algebraic points under repeated application of a polynomial or rational function. A fundamental goal is to describe arithmetic properties in terms of underlying geometric structures.
In mathematics, and particularly complex dynamics, the escaping set of an entire function ƒ consists of all points that tend to infinity under the repeated application of ƒ. That is, a complex number belongs to the escaping set if and only if the sequence defined by converges to infinity as gets large. The escaping set of is denoted by .

In the mathematical discipline known as complex dynamics, the Herman ring is a Fatou component where the rational function is conformally conjugate to an irrational rotation of the standard annulus.
In mathematics, a quasicircle is a Jordan curve in the complex plane that is the image of a circle under a quasiconformal mapping of the plane onto itself. Originally introduced independently by Pfluger (1961) and Tienari (1962), in the older literature they were referred to as quasiconformal curves, a terminology which also applied to arcs. In complex analysis and geometric function theory, quasicircles play a fundamental role in the description of the universal Teichmüller space, through quasisymmetric homeomorphisms of the circle. Quasicircles also play an important role in complex dynamical systems.
In mathematics, calculus on Euclidean space is a generalization of calculus of functions in one or several variables to calculus of functions on Euclidean space as well as a finite-dimensional real vector space. This calculus is also known as advanced calculus, especially in the United States. It is similar to multivariable calculus but is somehow more sophisticated in that it uses linear algebra more extensively and covers some concepts from differential geometry such as differential forms and Stokes' formula in terms of differential forms. This extensive use of linear algebra also allows a natural generalization of multivariable calculus to calculus on Banach spaces or topological vector spaces.
![This image illustrates the dynamics of
f
(
z
)
=
z
+
2
p
sin
[?]
(
z
)
{\displaystyle f(z)=z+2\pi \sin(z)}
; the Fatou set (consisting entirely of wandering domains) is shown in white, while the Julia set is shown in tones of gray. Wandering domains for the entire function f(z)=z+2psin(z).png](http://upload.wikimedia.org/wikipedia/commons/thumb/4/4f/Wandering_domains_for_the_entire_function_f%28z%29%3Dz%2B2%CF%80sin%28z%29.png/220px-Wandering_domains_for_the_entire_function_f%28z%29%3Dz%2B2%CF%80sin%28z%29.png)









