Noninterference is a strict multilevel security policy model, first described by Goguen and Meseguer in 1982 and developed further in 1984.
In simple terms, a computer is modeled as a machine with inputs and outputs. Inputs and outputs are classified as either low (low sensitivity, not highly classified) or high (sensitive, not to be viewed by uncleared individuals). A computer has the noninterference property if and only if any sequence of low inputs will produce the same low outputs, regardless of what the high level inputs are.
That is, if a low (uncleared) user is working on the machine, it will respond in exactly the same manner (on the low outputs) whether or not a high (cleared) user is working with sensitive data. The low user will not be able to acquire any information about the activities (if any) of the high user.
Let be a memory configuration, and let and be the projection of the memory to the low and high parts, respectively. Let be the function that compares the low parts of the memory configurations, i.e., iff . Let be the execution of the program starting with memory configuration and terminating with the memory configuration .
The definition of noninterference for a deterministic program is the following: [1]
This is a very strict policy, in that a computer system with covert channels may comply with, say, the Bell–LaPadula model, but will not comply with noninterference. The reverse could be true (under reasonable conditions, being that the system should have labelled files, etc.) except for the "No classified information at startup" exceptions noted below. However, noninterference has been shown to be stronger than nondeducibility.
This strictness comes with a price. It is very difficult to make a computer system with this property. There may be only one or two commercially available products that have been verified to comply with this policy, and these would essentially be as simple as switches and one-way information filters (although these could be arranged to provide useful behaviour).
If the computer has (at time = 0) any high (i.e., classified) information within it, or low users create high information subsequent to time=0 (so-called "write-up", which is allowed by many computer security policies), then the computer can legally leak all that high information to the low user, and can still be said to comply with the noninterference policy. The low user will not be able to learn anything about high user activities, but can learn about any high information that was created through means other than the actions of high users (von Oheimb, 2004).
Computer systems that comply with the Bell–LaPadula Model do not suffer from this problem since they explicitly forbid "read-up". Consequently, a computer system that complies with noninterference will not necessarily comply with the Bell–LaPadula Model. Thus, the Bell–LaPadula model and the noninterference model are incomparable: the Bell–LaPadula Model is stricter regarding read-up, and the noninterference model is stricter with respect to covert channels.
Some legitimate multilevel security activities treat individual data records (e.g., personal details) as sensitive, but allow statistical functions of the data (e.g., the mean, the total number) to be released more widely. This cannot be achieved with a noninterference machine.
The noninterference property requires that the system should not reveal any information about the high inputs from the observable output for various low inputs. However, one can argue that achieving noninterference is oftentimes not possible for a large class of practical systems, and moreover, it may not be desirable: programs need to reveal information that depends on the secret inputs, e.g. the output must be different when a user enters a correct credential vs. when she enters incorrect credentials. Shannon entropy, guessing entropy, and min-entropy are prevalent notions of quantitative information leakage that generalize noninterference. [2]
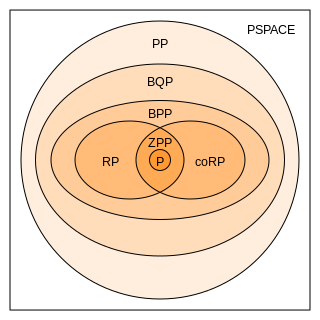
In computational complexity theory, bounded-error quantum polynomial time (BQP) is the class of decision problems solvable by a quantum computer in polynomial time, with an error probability of at most 1/3 for all instances. It is the quantum analogue to the complexity class BPP.
Pattern recognition is the task of assigning a class to an observation based on patterns extracted from data. While similar, pattern recognition (PR) is not to be confused with pattern machines (PM) which may possess (PR) capabilities but their primary function is to distinguish and create emergent pattern. PR has applications in statistical data analysis, signal processing, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Pattern recognition has its origins in statistics and engineering; some modern approaches to pattern recognition include the use of machine learning, due to the increased availability of big data and a new abundance of processing power.
Rate–distortion theory is a major branch of information theory which provides the theoretical foundations for lossy data compression; it addresses the problem of determining the minimal number of bits per symbol, as measured by the rate R, that should be communicated over a channel, so that the source can be approximately reconstructed at the receiver without exceeding an expected distortion D.
In electronics, a common-base amplifier is one of three basic single-stage bipolar junction transistor (BJT) amplifier topologies, typically used as a current buffer or voltage amplifier.
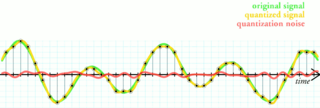
Quantization, in mathematics and digital signal processing, is the process of mapping input values from a large set to output values in a (countable) smaller set, often with a finite number of elements. Rounding and truncation are typical examples of quantization processes. Quantization is involved to some degree in nearly all digital signal processing, as the process of representing a signal in digital form ordinarily involves rounding. Quantization also forms the core of essentially all lossy compression algorithms.
The Bell–LaPadula model (BLP) is a state machine model used for enforcing access control in government and military applications. It was developed by David Elliott Bell, and Leonard J. LaPadula, subsequent to strong guidance from Roger R. Schell, to formalize the U.S. Department of Defense (DoD) multilevel security (MLS) policy. The model is a formal state transition model of computer security policy that describes a set of access control rules which use security labels on objects and clearances for subjects. Security labels range from the most sensitive, down to the least sensitive.
A commitment scheme is a cryptographic primitive that allows one to commit to a chosen value while keeping it hidden to others, with the ability to reveal the committed value later. Commitment schemes are designed so that a party cannot change the value or statement after they have committed to it: that is, commitment schemes are binding. Commitment schemes have important applications in a number of cryptographic protocols including secure coin flipping, zero-knowledge proofs, and secure computation.
In computational complexity theory, a complexity class is a set of computational problems "of related resource-based complexity". The two most commonly analyzed resources are time and memory.
In complexity theory, PP is the class of decision problems solvable by a probabilistic Turing machine in polynomial time, with an error probability of less than 1/2 for all instances. The abbreviation PP refers to probabilistic polynomial time. The complexity class was defined by Gill in 1977.
Multi-task learning (MTL) is a subfield of machine learning in which multiple learning tasks are solved at the same time, while exploiting commonalities and differences across tasks. This can result in improved learning efficiency and prediction accuracy for the task-specific models, when compared to training the models separately. Early versions of MTL were called "hints".
Multilevel security or multiple levels of security (MLS) is the application of a computer system to process information with incompatible classifications, permit access by users with different security clearances and needs-to-know, and prevent users from obtaining access to information for which they lack authorization. There are two contexts for the use of multilevel security.
Information flow in an information theoretical context is the transfer of information from a variable to a variable in a given process. Not all flows may be desirable; for example, a system should not leak any confidential information to public observers—as it is a violation of privacy on an individual level, or might cause major loss on a corporate level.
Quantum neural networks are computational neural network models which are based on the principles of quantum mechanics. The first ideas on quantum neural computation were published independently in 1995 by Subhash Kak and Ron Chrisley, engaging with the theory of quantum mind, which posits that quantum effects play a role in cognitive function. However, typical research in quantum neural networks involves combining classical artificial neural network models with the advantages of quantum information in order to develop more efficient algorithms. One important motivation for these investigations is the difficulty to train classical neural networks, especially in big data applications. The hope is that features of quantum computing such as quantum parallelism or the effects of interference and entanglement can be used as resources. Since the technological implementation of a quantum computer is still in a premature stage, such quantum neural network models are mostly theoretical proposals that await their full implementation in physical experiments.
In cryptography, a one-way compression function is a function that transforms two fixed-length inputs into a fixed-length output. The transformation is "one-way", meaning that it is difficult given a particular output to compute inputs which compress to that output. One-way compression functions are not related to conventional data compression algorithms, which instead can be inverted exactly or approximately to the original data.
A Wilson current mirror is a three-terminal circuit that accepts an input current at the input terminal and provides a "mirrored" current source or sink output at the output terminal. The mirrored current is a precise copy of the input current. It may be used as a Wilson current source by applying a constant bias current to the input branch as in Fig. 2. The circuit is named after George R. Wilson, an integrated circuit design engineer who worked for Tektronix. Wilson devised this configuration in 1967 when he and Barrie Gilbert challenged each other to find an improved current mirror overnight that would use only three transistors. Wilson won the challenge.
A queue machine, queue automaton, or pullup automaton (PUA) is a finite state machine with the ability to store and retrieve data from an infinite-memory queue. It is a model of computation equivalent to a Turing machine, and therefore it can process the same class of formal languages.
A randomness extractor, often simply called an "extractor", is a function, which being applied to output from a weak entropy source, together with a short, uniformly random seed, generates a highly random output that appears independent from the source and uniformly distributed. Examples of weakly random sources include radioactive decay or thermal noise; the only restriction on possible sources is that there is no way they can be fully controlled, calculated or predicted, and that a lower bound on their entropy rate can be established. For a given source, a randomness extractor can even be considered to be a true random number generator (TRNG); but there is no single extractor that has been proven to produce truly random output from any type of weakly random source.
Compartmental modelling of dendrites deals with multi-compartment modelling of the dendrites, to make the understanding of the electrical behavior of complex dendrites easier. Basically, compartmental modelling of dendrites is a very helpful tool to develop new biological neuron models. Dendrites are very important because they occupy the most membrane area in many of the neurons and give the neuron an ability to connect to thousands of other cells. Originally the dendrites were thought to have constant conductance and current but now it has been understood that they may have active Voltage-gated ion channels, which influences the firing properties of the neuron and also the response of neuron to synaptic inputs. Many mathematical models have been developed to understand the electric behavior of the dendrites. Dendrites tend to be very branchy and complex, so the compartmental approach to understand the electrical behavior of the dendrites makes it very useful.
Fuzzy extractors are a method that allows biometric data to be used as inputs to standard cryptographic techniques, to enhance computer security. "Fuzzy", in this context, refers to the fact that the fixed values required for cryptography will be extracted from values close to but not identical to the original key, without compromising the security required. One application is to encrypt and authenticate users records, using the biometric inputs of the user as a key.
In cryptography, a sponge function or sponge construction is any of a class of algorithms with finite internal state that take an input bit stream of any length and produce an output bit stream of any desired length. Sponge functions have both theoretical and practical uses. They can be used to model or implement many cryptographic primitives, including cryptographic hashes, message authentication codes, mask generation functions, stream ciphers, pseudo-random number generators, and authenticated encryption.
