In mathematics, logic, and computer science, a type system is a formal system in which every term has a "type" which defines its meaning and the operations that may be performed on it. Type theory is the academic study of type systems.

In lambda calculus, the Church–Rosser theorem states that, when applying reduction rules to terms, the ordering in which the reductions are chosen does not make a difference to the eventual result.
In programming language theory and proof theory, the Curry–Howard correspondence is the direct relationship between computer programs and mathematical proofs.
A typed lambda calculus is a typed formalism that uses the lambda-symbol to denote anonymous function abstraction. In this context, types are usually objects of a syntactic nature that are assigned to lambda terms; the exact nature of a type depends on the calculus considered. From a certain point of view, typed lambda calculi can be seen as refinements of the untyped lambda calculus, but from another point of view, they can also be considered the more fundamental theory and untyped lambda calculus a special case with only one type.
In theoretical computer science a bisimulation is a binary relation between state transition systems, associating systems that behave in the same way in that one system simulates the other and vice versa.
In mathematical logic and computer science, the calculus of constructions (CoC) is a type theory created by Thierry Coquand. It can serve as both a typed programming language and as constructive foundation for mathematics. For this second reason, the CoC and its variants have been the basis for Coq and other proof assistants.
System F, also known as the (Girard–Reynolds) polymorphic lambda calculus or the second-order lambda calculus, is a typed lambda calculus that differs from the simply typed lambda calculus by the introduction of a mechanism of universal quantification over types. System F thus formalizes the notion of parametric polymorphism in programming languages, and forms a theoretical basis for languages such as Haskell and ML. System F was discovered independently by logician Jean-Yves Girard (1972) and computer scientist John C. Reynolds (1974).
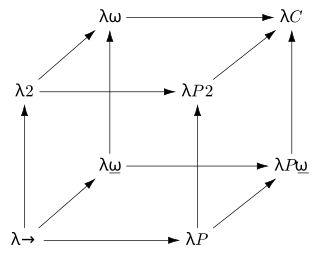
In mathematical logic and type theory, the λ-cube is a framework introduced by Henk Barendregt to investigate the different dimensions in which the calculus of constructions is a generalization of the simply typed λ-calculus. Each dimension of the cube corresponds to a new kind of dependency between terms and types. Here, "dependency" refers to the capacity of a term or type to bind a term or type. The respective dimensions of the λ-cube correspond to:
In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for (interactive) automated theorem proving. The first logical framework was Automath; however, the name of the idea comes from the more widely known Edinburgh Logical Framework, LF. Several more recent proof tools like Isabelle are based on this idea. Unlike a direct embedding, the logical framework approach allows many logics to be embedded in the same type system.
Variational Bayesian methods are a family of techniques for approximating intractable integrals arising in Bayesian inference and machine learning. They are typically used in complex statistical models consisting of observed variables as well as unknown parameters and latent variables, with various sorts of relationships among the three types of random variables, as might be described by a graphical model. As typical in Bayesian inference, the parameters and latent variables are grouped together as "unobserved variables". Variational Bayesian methods are primarily used for two purposes:
- To provide an analytical approximation to the posterior probability of the unobserved variables, in order to do statistical inference over these variables.
- To derive a lower bound for the marginal likelihood of the observed data. This is typically used for performing model selection, the general idea being that a higher marginal likelihood for a given model indicates a better fit of the data by that model and hence a greater probability that the model in question was the one that generated the data.
The simply typed lambda calculus, a form of type theory, is a typed interpretation of the lambda calculus with only one type constructor that builds function types. It is the canonical and simplest example of a typed lambda calculus. The simply typed lambda calculus was originally introduced by Alonzo Church in 1940 as an attempt to avoid paradoxical uses of the untyped lambda calculus, and it exhibits many desirable and interesting properties.

In mathematics, a complex torus is a particular kind of complex manifold M whose underlying smooth manifold is a torus in the usual sense. Here N must be the even number 2n, where n is the complex dimension of M.
In probability theory and statistics, the normal-gamma distribution is a bivariate four-parameter family of continuous probability distributions. It is the conjugate prior of a normal distribution with unknown mean and precision.
In programming language semantics, normalisation by evaluation (NBE) is a style of obtaining the normal form of terms in the λ-calculus by appealing to their denotational semantics. A term is first interpreted into a denotational model of the λ-term structure, and then a canonical representative is extracted by reifying the denotation. Such an essentially semantic approach differs from the more traditional syntactic description of normalisation as a reductions in a term rewrite system where β-reductions are allowed deep inside λ-terms.
In mathematics, particularly linear algebra, the Schur–Horn theorem, named after Issai Schur and Alfred Horn, characterizes the diagonal of a Hermitian matrix with given eigenvalues. It has inspired investigations and substantial generalizations in the setting of symplectic geometry. A few important generalizations are Kostant's convexity theorem, Atiyah–Guillemin–Sternberg convexity theorem, Kirwan convexity theorem.
In the fields of computer vision and image analysis, the scale-invariant feature operator is an algorithm to detect local features in images. The algorithm was published by Förstner et al. in 2009.
A Hindley–Milner (HM) type system is a classical type system for the lambda calculus with parametric polymorphism. It is also known as Damas–Milner or Damas–Hindley–Milner. It was first described by J. Roger Hindley and later rediscovered by Robin Milner. Luis Damas contributed a close formal analysis and proof of the method in his PhD thesis.
In rewriting, a reduction strategy or rewriting strategy is a relation specifying a rewrite for each object or term, compatible with a given reduction relation. Some authors use the term to refer to an evaluation strategy.
In mathematical logic, the intersection type discipline is a branch of type theory encompassing type systems that use the intersection type constructor to assign multiple types to a single term. In particular, if a term can be assigned both' the type and the type , then can be assigned the intersection type . Therefore, the intersection type constructor can be used to express finite heterogeneous ad hoc polymorphism . For example, the λ-term can be assigned the type in most intersection type systems, assuming for the term variable both the function type and the corresponding argument type .
Tau functions are an important ingredient in the modern theory of integrable systems, and have numerous applications in a variety of other domains. They were originally introduced by Ryogo Hirota in his direct method approach to soliton equations, based on expressing them in an equivalent bilinear form. The term Tau function, or -function, was first used systematically by Mikio Sato and his students in the specific context of the Kadomtsev–Petviashvili equation, and related integrable hierarchies. It is a central ingredient in the theory of solitons. Tau functions also appear as matrix model partition functions in the spectral theory of Random Matrices, and may also serve as generating functions, in the sense of combinatorics and enumerative geometry, especially in relation to moduli spaces of Riemann surfaces, and enumeration of branched coverings, or so-called Hurwitz numbers.











