In mathematics, the determinant is a scalar value that is a function of the entries of a square matrix. It allows characterizing some properties of the matrix and the linear map represented by the matrix. In particular, the determinant is nonzero if and only if the matrix is invertible, and the linear map represented by the matrix is an isomorphism. The determinant of a product of matrices is the product of their determinants . The determinant of a matrix A is denoted det(A), det A, or |A|.
In linear algebra, the rank of a matrix A is the dimension of the vector space generated by its columns. This corresponds to the maximal number of linearly independent columns of A. This, in turn, is identical to the dimension of the vector space spanned by its rows. Rank is thus a measure of the "nondegenerateness" of the system of linear equations and linear transformation encoded by A. There are multiple equivalent definitions of rank. A matrix's rank is one of its most fundamental characteristics.

In linear algebra, the column space of a matrix A is the span of its column vectors. The column space of a matrix is the image or range of the corresponding matrix transformation.
In linear algebra, a Toeplitz matrix or diagonal-constant matrix, named after Otto Toeplitz, is a matrix in which each descending diagonal from left to right is constant. For instance, the following matrix is a Toeplitz matrix:

In mathematics, a square matrix is a matrix with the same number of rows and columns. An n-by-n matrix is known as a square matrix of order . Any two square matrices of the same order can be added and multiplied.

In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal; that is, it switches the row and column indices of the matrix A by producing another matrix, often denoted by AT.

In mathematics, the orthogonal group in dimension n, denoted O(n), is the group of distance-preserving transformations of a Euclidean space of dimension n that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of n×n orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In linear algebra, the adjugate or classical adjoint of a square matrix is the transpose of its cofactor matrix. It is also occasionally known as adjunct matrix, though this nomenclature appears to have decreased in usage.
In linear algebra, an n-by-n square matrix A is called invertible, if there exists an n-by-n square matrix B such that
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows and columns. Minors obtained by removing just one row and one column from square matrices are required for calculating matrix cofactors, which in turn are useful for computing both the determinant and inverse of square matrices.
In mathematics, a block matrix or a partitioned matrix is a matrix that is interpreted as having been broken into sections called blocks or submatrices. Intuitively, a matrix interpreted as a block matrix can be visualized as the original matrix with a collection of horizontal and vertical lines, which break it up, or partition it, into a collection of smaller matrices. Any matrix may be interpreted as a block matrix in one or more ways, with each interpretation defined by how its rows and columns are partitioned.
In linear algebra, a tridiagonal matrix is a band matrix that has nonzero elements on the main diagonal, the first diagonal below this, and the first diagonal above the main diagonal only.
In mathematics, a unimodular matrixM is a square integer matrix having determinant +1 or −1. Equivalently, it is an integer matrix that is invertible over the integers: there is an integer matrix N that is its inverse. Thus every equation Mx = b, where M and b both have integer components and M is unimodular, has an integer solution. The n × n unimodular matrices form a group called the n × n general linear group over , which is denoted .
In mathematics, the kernel of a linear map, also known as the null space or nullspace, is the linear subspace of the domain of the map which is mapped to the zero vector. That is, given a linear map L : V → W between two vector spaces V and W, the kernel of L is the vector space of all elements v of V such that L(v) = 0, where 0 denotes the zero vector in W, or more symbolically:
Sylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of basis. Namely, if A is the symmetric matrix that defines the quadratic form, and S is any invertible matrix such that D = SAST is diagonal, then the number of negative elements in the diagonal of D is always the same, for all such S; and the same goes for the number of positive elements.
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression of the determinant of an n × n matrix B as a weighted sum of minors, which are the determinants of some (n − 1) × submatrices of B. Specifically, for every i,
In mathematics, especially linear algebra, an M-matrix is a Z-matrix with eigenvalues whose real parts are nonnegative. The set of non-singular M-matrices are a subset of the class of P-matrices, and also of the class of inverse-positive matrices. The name M-matrix was seemingly originally chosen by Alexander Ostrowski in reference to Hermann Minkowski, who proved that if a Z-matrix has all of its row sums positive, then the determinant of that matrix is positive.

In mathematics, a matrix is a rectangular array or table of numbers, symbols, or expressions, arranged in rows and columns. For example, the dimension of the matrix below is 2 × 3, because there are two rows and three columns:
In mathematics, the Haynsworth inertia additivity formula, discovered by Emilie Virginia Haynsworth (1916–1985), concerns the number of positive, negative, and zero eigenvalues of a Hermitian matrix and of block matrices into which it is partitioned.
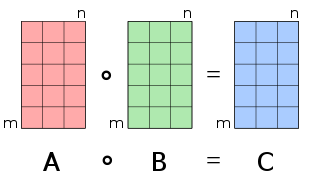
In mathematics, the Hadamard product is a binary operation that takes two matrices of the same dimensions and produces another matrix of the same dimension as the operands, where each element i, j is the product of elements i, j of the original two matrices. It is to be distinguished from the more common matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard or German mathematician Issai Schur.







