| Class | Nucleic acid structure prediction |
|---|---|
| Worst-case performance | |
| Worst-case space complexity |
The Nussinov algorithm is a nucleic acid structure prediction algorithm used in computational biology to predict the folding of an RNA molecule that makes use of dynamic programming principles. [1] The algorithm was developed by Ruth Nussinov in the late 1970s.
RNA origami occurs when an RNA molecule "folds" and binds to itself. This folding often determines the function of the RNA molecule. RNA folds at different levels, this algorithm predicts the secondary structure of the RNA.
We score a solution by counting the total number of paired bases. Thus, attempting to maximize the score that maximizes the total number of bonds between bases.
Consider an RNA sequence whose elements are taken from the set . Let us imagine we have an optimal solution to the subproblem of folding to , and an optimal solution for folding to . Now, to align to , we have two options:
Consider an RNA sequence of length such that .
Construct an matrix . Initialize such that
for .
will contain the maximum score for the subsequence . Now, fill in entries of up and to the right, so that
where
After this step, we have a matrix where represents the optimal score of the folding of .
To determine the structure of the folded RNA by traceback, we first create an empty list of pairs . We initialize with . Then, we follow one of three scenarios.
When the traceback finishes, contains all of the paired bases.
The Nussinov algorithm does not account for the three-dimensional shape of RNA, nor predict RNA pseudoknots. [2] Furthermore, in its basic form, it does not account for a minimum stem loop size. However, it is still useful as a fast algorithm for basic prediction of secondary structure.
Dynamic programming is both a mathematical optimization method and a computer programming method. The method was developed by Richard Bellman in the 1950s and has found applications in numerous fields, from aerospace engineering to economics.
Grammar theory to model symbol strings originated from work in computational linguistics aiming to understand the structure of natural languages. Probabilistic context free grammars (PCFGs) have been applied in probabilistic modeling of RNA structures almost 40 years after they were introduced in computational linguistics.
In computational linguistics and computer science, edit distance is a string metric, i.e. a way of quantifying how dissimilar two strings are to one another, that is measured by counting the minimum number of operations required to transform one string into the other. Edit distances find applications in natural language processing, where automatic spelling correction can determine candidate corrections for a misspelled word by selecting words from a dictionary that have a low distance to the word in question. In bioinformatics, it can be used to quantify the similarity of DNA sequences, which can be viewed as strings of the letters A, C, G and T.
Structural alignment attempts to establish homology between two or more polymer structures based on their shape and three-dimensional conformation. This process is usually applied to protein tertiary structures but can also be used for large RNA molecules. In contrast to simple structural superposition, where at least some equivalent residues of the two structures are known, structural alignment requires no a priori knowledge of equivalent positions. Structural alignment is a valuable tool for the comparison of proteins with low sequence similarity, where evolutionary relationships between proteins cannot be easily detected by standard sequence alignment techniques. Structural alignment can therefore be used to imply evolutionary relationships between proteins that share very little common sequence. However, caution should be used in using the results as evidence for shared evolutionary ancestry because of the possible confounding effects of convergent evolution by which multiple unrelated amino acid sequences converge on a common tertiary structure.
The Needleman–Wunsch algorithm is an algorithm used in bioinformatics to align protein or nucleotide sequences. It was one of the first applications of dynamic programming to compare biological sequences. The algorithm was developed by Saul B. Needleman and Christian D. Wunsch and published in 1970. The algorithm essentially divides a large problem into a series of smaller problems, and it uses the solutions to the smaller problems to find an optimal solution to the larger problem. It is also sometimes referred to as the optimal matching algorithm and the global alignment technique. The Needleman–Wunsch algorithm is still widely used for optimal global alignment, particularly when the quality of the global alignment is of the utmost importance. The algorithm assigns a score to every possible alignment, and the purpose of the algorithm is to find all possible alignments having the highest score.
Random forests or random decision forests is an ensemble learning method for classification, regression and other tasks that operates by constructing a multitude of decision trees at training time. For classification tasks, the output of the random forest is the class selected by most trees. For regression tasks, the mean or average prediction of the individual trees is returned. Random decision forests correct for decision trees' habit of overfitting to their training set. Random forests generally outperform decision trees, but their accuracy is lower than gradient boosted trees. However, data characteristics can affect their performance.
The Smith–Waterman algorithm performs local sequence alignment; that is, for determining similar regions between two strings of nucleic acid sequences or protein sequences. Instead of looking at the entire sequence, the Smith–Waterman algorithm compares segments of all possible lengths and optimizes the similarity measure.
Szemerédi's regularity lemma is one of the most powerful tools in extremal graph theory, particularly in the study of large dense graphs. It states that the vertices of every large enough graph can be partitioned into a bounded number of parts so that the edges between different parts behave almost randomly.
In mathematical optimization, the Karush–Kuhn–Tucker (KKT) conditions, also known as the Kuhn–Tucker conditions, are first derivative tests for a solution in nonlinear programming to be optimal, provided that some regularity conditions are satisfied.
In computational phylogenetics, tree alignment is a computational problem concerned with producing multiple sequence alignments, or alignments of three or more sequences of DNA, RNA, or protein. Sequences are arranged into a phylogenetic tree, modeling the evolutionary relationships between species or taxa. The edit distances between sequences are calculated for each of the tree's internal vertices, such that the sum of all edit distances within the tree is minimized. Tree alignment can be accomplished using one of several algorithms with various trade-offs between manageable tree size and computational effort.
Nucleic acid structure prediction is a computational method to determine secondary and tertiary nucleic acid structure from its sequence. Secondary structure can be predicted from one or several nucleic acid sequences. Tertiary structure can be predicted from the sequence, or by comparative modeling.
In computer science, Hirschberg's algorithm, named after its inventor, Dan Hirschberg, is a dynamic programming algorithm that finds the optimal sequence alignment between two strings. Optimality is measured with the Levenshtein distance, defined to be the sum of the costs of insertions, replacements, deletions, and null actions needed to change one string into the other. Hirschberg's algorithm is simply described as a more space-efficient version of the Needleman–Wunsch algorithm that uses divide and conquer. Hirschberg's algorithm is commonly used in computational biology to find maximal global alignments of DNA and protein sequences.
The Kabsch algorithm, named after Wolfgang Kabsch, is a method for calculating the optimal rotation matrix that minimizes the RMSD between two paired sets of points. It is useful in graphics, cheminformatics to compare molecular structures, and also bioinformatics for comparing protein structures.
In bioinformatics, Stemloc is an open source software for multiple RNA sequence alignment and RNA structure prediction based on probabilistic models of RNA structure known as Pair stochastic context-free grammars. Stemloc attempts to simultaneously predict and align the structure of RNA sequences with an improved time and space cost compared to previous methods with the same motive. The resulting software implements constrained versions of the Sankoff algorithm by introducing both fold and alignment constraints, which reduces processor and memory usage and allows for larger RNA sequences to be analyzed on commodity hardware. Stemloc was written in 2004 by Ian Holmes.
In mathematics, low-rank approximation is a minimization problem, in which the cost function measures the fit between a given matrix and an approximating matrix, subject to a constraint that the approximating matrix has reduced rank. The problem is used for mathematical modeling and data compression. The rank constraint is related to a constraint on the complexity of a model that fits the data. In applications, often there are other constraints on the approximating matrix apart from the rank constraint, e.g., non-negativity and Hankel structure.
Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry represents the rating of movie by customer , if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the document-term matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.
Ruth Nussinov is an Israeli-American biologist who works as a Professor in the Department of Human Genetics, School of Medicine at Tel Aviv University and is the Senior Principal Scientist and Principal Investigator at the National Cancer Institute, National Institutes of Health. Nussinov is also the Editor in Chief for the journal PLOS Computational Biology.
A neutral network is a set of genes all related by point mutations that have equivalent function or fitness. Each node represents a gene sequence and each line represents the mutation connecting two sequences. Neutral networks can be thought of as high, flat plateaus in a fitness landscape. During neutral evolution, genes can randomly move through neutral networks and traverse regions of sequence space which may have consequences for robustness and evolvability.
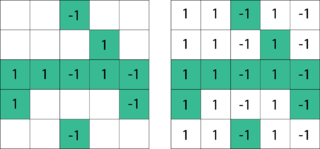
The Ruzzo–Tompa algorithm or the RT algorithm is a linear-time algorithm for finding all non-overlapping, contiguous, maximal scoring subsequences in a sequence of real numbers. The Ruzzo–Tompa algorithm was proposed by Walter L. Ruzzo and Martin Tompa. This algorithm is an improvement over previously known quadratic time algorithms. The maximum scoring subsequence from the set produced by the algorithm is also a solution to the maximum subarray problem.
