
A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, 1 × 5 or 5 × 1, involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order.
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on. In a finite continued fraction, the iteration/recursion is terminated after finitely many steps by using an integer in lieu of another continued fraction. In contrast, an infinite continued fraction is an infinite expression. In either case, all integers in the sequence, other than the first, must be positive. The integers are called the coefficients or terms of the continued fraction.
In mathematics, the harmonic series is the infinite series formed by summing all positive unit fractions:

Liber Abaci is a historic 1202 Latin manuscript on arithmetic by Leonardo of Pisa, posthumously known as Fibonacci.

An Egyptian fraction is a finite sum of distinct unit fractions, such as
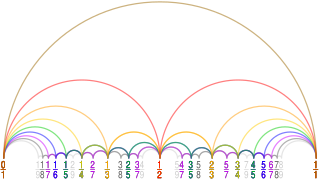
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions, either between 0 and 1, or without this restriction, which when in lowest terms have denominators less than or equal to n, arranged in order of increasing size.
A unit fraction is a rational number written as a fraction where the numerator is one and the denominator is a positive integer. A unit fraction is therefore the reciprocal of a positive integer, 1/n. Examples are 1/1, 1/2, 1/3, 1/4, 1/5, etc.
Mahāvīra was a 9th-century Jain mathematician possibly born in Mysore, in India. He authored Gaṇitasārasan̄graha or the Compendium on the gist of Mathematics in 850 AD. He was patronised by the Rashtrakuta king Amoghavarsha. He separated astrology from mathematics. It is the earliest Indian text entirely devoted to mathematics. He expounded on the same subjects on which Aryabhata and Brahmagupta contended, but he expressed them more clearly. His work is a highly syncopated approach to algebra and the emphasis in much of his text is on developing the techniques necessary to solve algebraic problems. He is highly respected among Indian mathematicians, because of his establishment of terminology for concepts such as equilateral, and isosceles triangle; rhombus; circle and semicircle. Mahāvīra's eminence spread throughout South India and his books proved inspirational to other mathematicians in Southern India. It was translated into the Telugu language by Pavuluri Mallana as Saara Sangraha Ganitamu.

In number theory, a practical number or panarithmic number is a positive integer such that all smaller positive integers can be represented as sums of distinct divisors of . For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2.

A fraction represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight-fifths, three-quarters. A common, vulgar, or simple fraction consists of a numerator, displayed above a line, and a non-zero denominator, displayed below that line. Numerators and denominators are also used in fractions that are not common, including compound fractions, complex fractions, and mixed numerals.
The Erdős–Straus conjecture is an unproven statement in number theory. The conjecture is that, for every integer that is 2 or more, there exist positive integers , , and for which
The Engel expansion of a positive real number x is the unique non-decreasing sequence of positive integers such that
A decimal representation of a non-negative real number r is its expression as a sequence of symbols consisting of decimal digits traditionally written with a single separator:
In number theory, Sylvester's sequence is an integer sequence in which each term of the sequence is the product of the previous terms, plus one. The first few terms of the sequence are
In mathematics, the greedy algorithm for Egyptian fractions is a greedy algorithm, first described by Fibonacci, for transforming rational numbers into Egyptian fractions. An Egyptian fraction is a representation of an irreducible fraction as a sum of distinct unit fractions, such as 5/6 = 1/2 + 1/3. As the name indicates, these representations have been used as long ago as ancient Egypt, but the first published systematic method for constructing such expansions is described in the Liber Abaci (1202) of Leonardo of Pisa (Fibonacci). It is called a greedy algorithm because at each step the algorithm chooses greedily the largest possible unit fraction that can be used in any representation of the remaining fraction.
The Egyptian Mathematical Leather Roll (EMLR) is a 10 × 17 in (25 × 43 cm) leather roll purchased by Alexander Henry Rhind in 1858. It was sent to the British Museum in 1864, along with the Rhind Mathematical Papyrus, but it was not chemically softened and unrolled until 1927.

Rod calculus or rod calculation was the mechanical method of algorithmic computation with counting rods in China from the Warring States to Ming dynasty before the counting rods were increasingly replaced by the more convenient and faster abacus. Rod calculus played a key role in the development of Chinese mathematics to its height in Song Dynasty and Yuan Dynasty, culminating in the invention of polynomial equations of up to four unknowns in the work of Zhu Shijie.
The Rhind Mathematical Papyrus, an ancient Egyptian mathematical work, includes a mathematical table for converting rational numbers of the form 2/n into Egyptian fractions, the form the Egyptians used to write fractional numbers. The text describes the representation of 50 rational numbers. It was written during the Second Intermediate Period of Egypt by Ahmes, the first writer of mathematics whose name is known. Aspects of the document may have been copied from an unknown 1850 BCE text.
The Lahun Mathematical Papyri is an ancient Egyptian mathematical text. It forms part of the Kahun Papyri, which was discovered at El-Lahun by Flinders Petrie during excavations of a workers' town near the pyramid of the 12th dynasty pharaoh Sesostris II. The Kahun Papyri are a collection of texts including administrative texts, medical texts, veterinarian texts and six fragments devoted to mathematics.
Ganita Kaumudi is a treatise on mathematics written by Indian mathematician Narayana Pandita in 1356. It was an arithmetical treatise alongside the other algebraic treatise called "Bijganita Vatamsa" by Narayana Pandit. It was written as a commentary on the Līlāvatī by Bhāskara II.




















