One in ten rule

Last updated

In statistics, the one in ten rule is a rule of thumb for how many predictor parameters can be estimated from data when doing regression analysis (in particular proportional hazards models in survival analysis and logistic regression) while keeping the risk of overfitting and finding spurious correlations low. The rule states that one predictive variable can be studied for every ten events. [1] [2] [3] [4] For logistic regression the number of events is given by the size of the smallest of the outcome categories, and for survival analysis it is given by the number of uncensored events. [3] In other words: for each feature we need 10 observations/labels.

Contents

For example, if a sample of 200 patients is studied and 20 patients die during the study (so that 180 patients survive), the one in ten rule implies that two pre-specified predictors can reliably be fitted to the total data. Similarly, if 100 patients die during the study (so that 100 patients survive), ten pre-specified predictors can be fitted reliably. If more are fitted, the rule implies that overfitting is likely and the results will not predict well outside the training data. It is not uncommon to see the 1:10 rule violated in fields with many variables (e.g. gene expression studies in cancer), decreasing the confidence in reported findings. [5]

Improvements

A "one in 20 rule" has been suggested, indicating the need for shrinkage of regression coefficients, and a "one in 50 rule" for stepwise selection with the default p-value of 5%. [4] [6] Other studies, however, show that the one in ten rule may be too conservative as a general recommendation and that five to nine events per predictor can be enough, depending on the research question. [7]

More recently, a study has shown that the ratio of events per predictive variable is not a reliable statistic for estimating the minimum number of events for estimating a logistic prediction model. [8] Instead, the number of predictor variables, the total sample size (events + non-events) and the events fraction (events / total sample size) can be used to calculate the expected prediction error of the model that is to be developed. [9] One can then estimate the required sample size to achieve an expected prediction error that is smaller than a predetermined allowable prediction error value. [9]

Alternatively, three requirements for prediction model estimation have been suggested: the model should have a global shrinkage factor of ≥ .9, an absolute difference of ≤ .05 in the model's apparent and adjusted Nagelkerke R2, and a precise estimation of the overall risk or rate in the target population. [10] The necessary sample size and number of events for model development are then given by the values that meet these requirements. [10]

Other modalities

For highly correlated input data the one-in-10 rule (10 observations or labels needed per feature) may not be directly applicable due to the high correlation of the features: For images there is a rule of thumb that per class 1000 examples are needed [11] . This would mean that for a binary classification of images (with fictive 1000 pixel x 1000 pixel per image, i.e. 1 000 000 features per image), we would only require 2000 labels /1 000 0000 pixel = 0.002 labels per pixel or 0.002 labels per feature. This is however only due to the high (spatial) correlation of pixels.

Literature

Related Research Articles

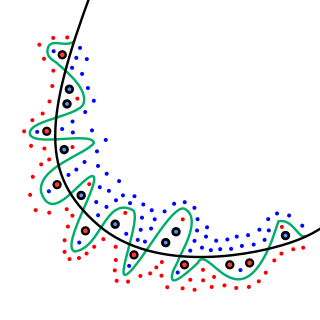
<span class="mw-page-title-main">Overfitting</span> Flaw in mathematical modelling

In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfitted model is a mathematical model that contains more parameters than can be justified by the data. In a mathematical sense, these parameters represent the degree of a polynomial. The essence of overfitting is to have unknowingly extracted some of the residual variation as if that variation represented underlying model structure.

<span class="mw-page-title-main">Logistic regression</span> Statistical model for a binary dependent variable

In statistics, the logistic model is a statistical model that models the log-odds of an event as a linear combination of one or more independent variables. In regression analysis, logistic regression estimates the parameters of a logistic model. In binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable or a continuous variable. The corresponding probability of the value labeled "1" can vary between 0 and 1, hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odds scale is called a logit, from logistic unit, hence the alternative names. See § Background and § Definition for formal mathematics, and § Example for a worked example.

<span class="mw-page-title-main">Prediction</span> Statement about a future event

A prediction or forecast is a statement about a future event or about future data. Predictions are often, but not always, based upon experience or knowledge of forecasters. There is no universal agreement about the exact difference between "prediction" and "estimation"; different authors and disciplines ascribe different connotations.

<span class="mw-page-title-main">Cross-validation (statistics)</span> Statistical model validation technique

Cross-validation, sometimes called rotation estimation or out-of-sample testing, is any of various similar model validation techniques for assessing how the results of a statistical analysis will generalize to an independent data set. Cross-validation includes resampling and sample splitting methods that use different portions of the data to test and train a model on different iterations. It is often used in settings where the goal is prediction, and one wants to estimate how accurately a predictive model will perform in practice. It can also be used to assess the quality of a fitted model and the stability of its parameters.

<span class="mw-page-title-main">Regression analysis</span> Set of statistical processes for estimating the relationships among variables

In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable and one or more independent variables. The most common form of regression analysis is linear regression, in which one finds the line that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line that minimizes the sum of squared differences between the true data and that line. For specific mathematical reasons, this allows the researcher to estimate the conditional expectation of the dependent variable when the independent variables take on a given set of values. Less common forms of regression use slightly different procedures to estimate alternative location parameters or estimate the conditional expectation across a broader collection of non-linear models.

<span class="mw-page-title-main">Linear discriminant analysis</span> Method used in statistics, pattern recognition, and other fields

Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later classification.

<span class="mw-page-title-main">Coefficient of determination</span> Indicator for how well data points fit a line or curve

In statistics, the coefficient of determination, denoted R2 or r2 and pronounced "R squared", is the proportion of the variation in the dependent variable that is predictable from the independent variable(s).

When classification is performed by a computer, statistical methods are normally used to develop the algorithm.

In statistics, unit-weighted regression is a simplified and robust version of multiple regression analysis where only the intercept term is estimated. That is, it fits a model

In statistics, overdispersion is the presence of greater variability in a data set than would be expected based on a given statistical model.

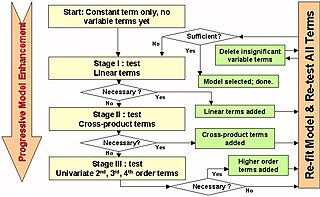
<span class="mw-page-title-main">Stepwise regression</span> Method of statistical factor analysis

In statistics, stepwise regression is a method of fitting regression models in which the choice of predictive variables is carried out by an automatic procedure. In each step, a variable is considered for addition to or subtraction from the set of explanatory variables based on some prespecified criterion. Usually, this takes the form of a forward, backward, or combined sequence of F-tests or t-tests.

<span class="mw-page-title-main">Recursive partitioning</span>

Recursive partitioning is a statistical method for multivariable analysis. Recursive partitioning creates a decision tree that strives to correctly classify members of the population by splitting it into sub-populations based on several dichotomous independent variables. The process is termed recursive because each sub-population may in turn be split an indefinite number of times until the splitting process terminates after a particular stopping criterion is reached.

In statistics, regression validation is the process of deciding whether the numerical results quantifying hypothesized relationships between variables, obtained from regression analysis, are acceptable as descriptions of the data. The validation process can involve analyzing the goodness of fit of the regression, analyzing whether the regression residuals are random, and checking whether the model's predictive performance deteriorates substantially when applied to data that were not used in model estimation.

Within statistics, oversampling and undersampling in data analysis are techniques used to adjust the class distribution of a data set. These terms are used both in statistical sampling, survey design methodology and in machine learning.

The Hosmer–Lemeshow test is a statistical test for goodness of fit and calibration for logistic regression models. It is used frequently in risk prediction models. The test assesses whether or not the observed event rates match expected event rates in subgroups of the model population. The Hosmer–Lemeshow test specifically identifies subgroups as the deciles of fitted risk values. Models for which expected and observed event rates in subgroups are similar are called well calibrated.

In machine learning, Platt scaling or Platt calibration is a way of transforming the outputs of a classification model into a probability distribution over classes. The method was invented by John Platt in the context of support vector machines, replacing an earlier method by Vapnik, but can be applied to other classification models. Platt scaling works by fitting a logistic regression model to a classifier's scores.

Individual participant data is raw data from individual participants, and is often used in the context of meta-analysis.

Ewout W. Steyerberg is Professor of Clinical Biostatistics and Medical Decision Making at Leiden University Medical Center and a Professor of Medical Decision Making at Erasmus MC. He is interested in a wide range of statistical methods for medical research, but is mainly known for his seminal work on prediction modeling, which was stimulated by various research grants including a fellowship from the Royal Netherlands Academy of Arts and Sciences (KNAW). Steyerberg is one of the most cited researchers from the Netherlands. He has published over 1000 peer-reviewed articles according to PubMed, many in collaboration with clinical researchers, both in methodological and medical journals. His h-index exceeds 150 according to Google Scholar.

CP-GEP is a non-invasive prediction model for cutaneous melanoma patients that combines clinicopathologic (CP) variables with gene expression profiling (GEP). CP-GEP is able to identify cutaneous melanoma patients at low-risk for nodal metastasis who may forgo the sentinel lymph node biopsy (SLNB) procedure. The CP-GEP model was developed by the Mayo Clinic and SkylineDx BV, and it has been clinically validated in multiple studies.

References

  1. ↑ Harrell, F. E. Jr.; Lee, K. L.; Califf, R. M.; Pryor, D. B.; Rosati, R. A. (1984). "Regression modelling strategies for improved prognostic prediction". Stat Med . 3 (2): 143–52. doi:10.1002/sim.4780030207. PMID   6463451.
  2. ↑ Harrell, F. E. Jr.; Lee, K. L.; Mark, D. B. (1996). "Multivariable prognostic models: issues in developing models, evaluating assumptions and adequacy, and measuring and reducing errors" (PDF). Stat Med . 15 (4): 361–87. doi:10.1002/(sici)1097-0258(19960229)15:4<361::aid-sim168>3.0.co;2-4. PMID   8668867.
  3. 1 2 Peduzzi, Peter; Concato, John; Kemper, Elizabeth; Holford, Theodore R.; Feinstein, Alvan R. (1996). "A simulation study of the number of events per variable in logistic regression analysis". Journal of Clinical Epidemiology. 49 (12): 1373–1379. doi: 10.1016/s0895-4356(96)00236-3 . PMID   8970487.
  4. 1 2 "Chapter 8: Statistical Models for Prognostication: Problems with Regression Models". Archived from the original on October 31, 2004. Retrieved 2013-10-11.{{cite web}}: CS1 maint: bot: original URL status unknown (link)
  5. ↑ Ernest S. Shtatland, Ken Kleinman, Emily M. Cain. Model building in Proc PHREG with automatic variable selection and information criteria. Paper 206–30 in SUGI 30 Proceedings, Philadelphia, Pennsylvania April 10–13, 2005. http://www2.sas.com/proceedings/sugi30/206-30.pdf
  6. ↑ Steyerberg, E. W.; Eijkemans, M. J.; Harrell, F. E. Jr.; Habbema, J. D. (2000). "Prognostic modelling with logistic regression analysis: a comparison of selection and estimation methods in small data sets". Stat Med . 19 (8): 1059–1079. doi:10.1002/(sici)1097-0258(20000430)19:8<1059::aid-sim412>3.0.co;2-0. PMID   10790680.
  7. ↑ Vittinghoff, E.; McCulloch, C. E. (2007). "Relaxing the Rule of Ten Events per Variable in Logistic and Cox Regression". American Journal of Epidemiology. 165 (6): 710–718. doi: 10.1093/aje/kwk052 . PMID   17182981.
  8. ↑ van Smeden, Maarten; de Groot, Joris A. H.; Moons, Karel G. M.; Collins, Gary S.; Altman, Douglas G.; Eijkemans, Marinus J. C.; Reitsma, Johannes B. (2016-11-24). "No rationale for 1 variable per 10 events criterion for binary logistic regression analysis". BMC Medical Research Methodology. 16 (1): 163. doi: 10.1186/s12874-016-0267-3 . ISSN   1471-2288. PMC   5122171 . PMID   27881078.
  9. 1 2 van Smeden, Maarten; Moons, Karel Gm; de Groot, Joris Ah; Collins, Gary S.; Altman, Douglas G.; Eijkemans, Marinus Jc; Reitsma, Johannes B. (2018-01-01). "Sample size for binary logistic prediction models: Beyond events per variable criteria". Statistical Methods in Medical Research. 28 (8): 2455–2474. doi: 10.1177/0962280218784726 . ISSN   1477-0334. PMC   6710621 . PMID   29966490.
  10. 1 2 Riley, Richard D.; Snell, Kym IE; Ensor, Joie; Burke, Danielle L.; Jr, Frank E. Harrell; Moons, Karel GM; Collins, Gary S. (2018). "Minimum sample size for developing a multivariable prediction model: PART II - binary and time-to-event outcomes". Statistics in Medicine. 38 (7): 1276–1296. doi:10.1002/sim.7992. ISSN   1097-0258. PMC   6519266 . PMID   30357870.
  11. ↑ Applications of Machine Learning and Artificial Intelligence in Education. (2022). USA: IGI Global. Page 53, https://www.google.de/books/edition/Applications_of_Machine_Learning_and_Art/l59lEAAAQBAJ?hl=de&gbpv=1&dq=%22one%20in%20ten%20rule%22%20%20images%20machine%20learning&pg=PA53
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.