
In the theory of computational complexity, the travelling salesman problem (TSP) asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.

A minimum spanning tree (MST) or minimum weight spanning tree is a subset of the edges of a connected, edge-weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight. That is, it is a spanning tree whose sum of edge weights is as small as possible. More generally, any edge-weighted undirected graph has a minimum spanning forest, which is a union of the minimum spanning trees for its connected components.

A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally optimal solutions that approximate a globally optimal solution in a reasonable amount of time.
An integer programming problem is a mathematical optimization or feasibility program in which some or all of the variables are restricted to be integers. In many settings the term refers to integer linear programming (ILP), in which the objective function and the constraints are linear.

Combinatorial optimization is a subfield of mathematical optimization that consists of finding an optimal object from a finite set of objects, where the set of feasible solutions is discrete or can be reduced to a discrete set. Typical combinatorial optimization problems are the travelling salesman problem ("TSP"), the minimum spanning tree problem ("MST"), and the knapsack problem. In many such problems, such as the ones previously mentioned, exhaustive search is not tractable, and so specialized algorithms that quickly rule out large parts of the search space or approximation algorithms must be resorted to instead.
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there are also many approximation algorithms that provide an additive guarantee on the quality of the returned solution. A notable example of an approximation algorithm that provides both is the classic approximation algorithm of Lenstra, Shmoys and Tardos for scheduling on unrelated parallel machines.

A Euclidean minimum spanning tree of a finite set of points in the Euclidean plane or higher-dimensional Euclidean space connects the points by a system of line segments with the points as endpoints, minimizing the total length of the segments. In it, any two points can reach each other along a path through the line segments. It can be found as the minimum spanning tree of a complete graph with the points as vertices and the Euclidean distances between points as edge weights.
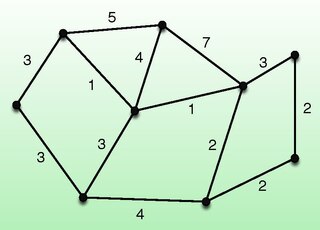
The k-minimum spanning tree problem, studied in theoretical computer science, asks for a tree of minimum cost that has exactly k vertices and forms a subgraph of a larger graph. It is also called the k-MST or edge-weighted k-cardinality tree. Finding this tree is NP-hard, but it can be approximated to within a constant approximation ratio in polynomial time.
The Christofides algorithm or Christofides–Serdyukov algorithm is an algorithm for finding approximate solutions to the travelling salesman problem, on instances where the distances form a metric space . It is an approximation algorithm that guarantees that its solutions will be within a factor of 3/2 of the optimal solution length, and is named after Nicos Christofides and Anatoliy Serdyukov. Christofides published the algorithm in 1976; Serdyukov discovered it independently in 1976 but published it in 1978.
Algorithmic game theory (AGT) is an area in the intersection of game theory and computer science, with the objective of understanding and design of algorithms in strategic environments.

David Bernard Shmoys is a Professor in the School of Operations Research and Information Engineering and the Department of Computer Science at Cornell University. He obtained his Ph.D. from the University of California, Berkeley in 1984. His major focus has been in the design and analysis of algorithms for discrete optimization problems.
In graph theory, the metric k-center problem or vertex k-center problem is a classical combinatorial optimization problem studied in theoretical computer science that is NP-hard. Given n cities with specified distances, one wants to build k warehouses in different cities and minimize the maximum distance of a city to a warehouse. In graph theory, this means finding a set of k vertices for which the largest distance of any point to its closest vertex in the k-set is minimum. The vertices must be in a metric space, providing a complete graph that satisfies the triangle inequality. It has application in facility location and clustering.
In computer science and operations research, randomized rounding is a widely used approach for designing and analyzing approximation algorithms.
The rectilinear Steiner tree problem, minimum rectilinear Steiner tree problem (MRST), or rectilinear Steiner minimum tree problem (RSMT) is a variant of the geometric Steiner tree problem in the plane, in which the Euclidean distance is replaced with the rectilinear distance. The problem may be formally stated as follows: given n points in the plane, it is required to interconnect them all by a shortest network which consists only of vertical and horizontal line segments. It can be shown that such a network is a tree whose vertices are the input points plus some extra points.
In computer science, the minimum routing cost spanning tree of a weighted graph is a spanning tree minimizing the sum of pairwise distances between vertices in the tree. It is also called the optimum distance spanning tree, shortest total path length spanning tree, minimum total distance spanning tree, or minimum average distance spanning tree. In an unweighted graph, this is the spanning tree of minimum Wiener index. Hu (1974) writes that the problem of constructing these trees was proposed by Francesco Maffioli.
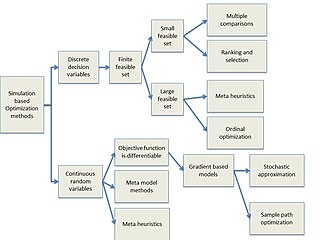
Simulation-based optimization integrates optimization techniques into simulation modeling and analysis. Because of the complexity of the simulation, the objective function may become difficult and expensive to evaluate. Usually, the underlying simulation model is stochastic, so that the objective function must be estimated using statistical estimation techniques.
In the study of hierarchical clustering, Dasgupta's objective is a measure of the quality of a clustering, defined from a similarity measure on the elements to be clustered. It is named after Sanjoy Dasgupta, who formulated it in 2016. Its key property is that, when the similarity comes from an ultrametric space, the optimal clustering for this quality measure follows the underlying structure of the ultrametric space. In this sense, clustering methods that produce good clusterings for this objective can be expected to approximate the ground truth underlying the given similarity measure.
In computer science, multiway number partitioning is the problem of partitioning a multiset of numbers into a fixed number of subsets, such that the sums of the subsets are as similar as possible. It was first presented by Ronald Graham in 1969 in the context of the identical-machines scheduling problem. The problem is parametrized by a positive integer k, and called k-way number partitioning. The input to the problem is a multiset S of numbers, whose sum is k*T.
Unrelated-machines scheduling is an optimization problem in computer science and operations research. It is a variant of optimal job scheduling. We need to schedule n jobs J1, J2, ..., Jn on m different machines, such that a certain objective function is optimized. The time that machine i needs in order to process job j is denoted by pi,j. The term unrelated emphasizes that there is no relation between values of pi,j for different i and j. This is in contrast to two special cases of this problem: uniform-machines scheduling - in which pi,j = pi / sj, and identical-machines scheduling - in which pi,j = pi.






