Automated theorem proving is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a major impetus for the development of computer science.
Knowledge representation and reasoning is the field of artificial intelligence (AI) dedicated to representing information about the world in a form that a computer system can use to solve complex tasks such as diagnosing a medical condition or having a dialog in a natural language. Knowledge representation incorporates findings from psychology about how humans solve problems, and represent knowledge in order to design formalisms that will make complex systems easier to design and build. Knowledge representation and reasoning also incorporates findings from logic to automate various kinds of reasoning.

ACL2 is a software system consisting of a programming language, an extensible theory in a first-order logic, and an automated theorem prover. ACL2 is designed to support automated reasoning in inductive logical theories, mostly for software and hardware verification. The input language and implementation of ACL2 are written in Common Lisp. ACL2 is free and open-source software.
E is a high-performance theorem prover for full first-order logic with equality. It is based on the equational superposition calculus and uses a purely equational paradigm. It has been integrated into other theorem provers and it has been among the best-placed systems in several theorem proving competitions. E is developed by Stephan Schulz, originally in the Automated Reasoning Group at TU Munich, now at Baden-Württemberg Cooperative State University Stuttgart.

In artificial intelligence, symbolic artificial intelligence is the term for the collection of all methods in artificial intelligence research that are based on high-level symbolic (human-readable) representations of problems, logic and search. Symbolic AI used tools such as logic programming, production rules, semantic nets and frames, and it developed applications such as knowledge-based systems, symbolic mathematics, automated theorem provers, ontologies, the semantic web, and automated planning and scheduling systems. The Symbolic AI paradigm led to seminal ideas in search, symbolic programming languages, agents, multi-agent systems, the semantic web, and the strengths and limitations of formal knowledge and reasoning systems.
Paradox is a finite-domain model finder for pure first-order logic (FOL) with equality developed by Koen Lindström Claessen and Niklas Sörensson at the Chalmers University of Technology. It can a participate as part of an automated theorem proving system. The software is primarily written in the Haskell programming language. It is released under the terms of the GNU General Public License and is free.

In computer science and mathematical logic, a proof assistant or interactive theorem prover is a software tool to assist with the development of formal proofs by human-machine collaboration. This involves some sort of interactive proof editor, or other interface, with which a human can guide the search for proofs, the details of which are stored in, and some steps provided by, a computer.
Carew Arthur Meredith, usually cited as C. A. Meredith, was an influential Irish logician, who worked in Trinity College, Dublin from 1943 to 1964. His work on condensed detachment is influential in modern research.
Condensed detachment is a method of finding the most general possible conclusion given two formal logical statements. It was developed by the Irish logician Carew Meredith in the 1950s and inspired by the work of Łukasiewicz.
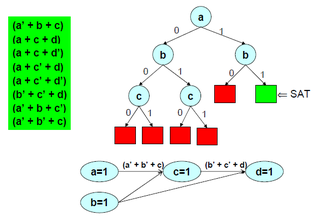
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solving the CNF-SAT problem.
In computer science, in particular in knowledge representation and reasoning and metalogic, the area of automated reasoning is dedicated to understanding different aspects of reasoning. The study of automated reasoning helps produce computer programs that allow computers to reason completely, or nearly completely, automatically. Although automated reasoning is considered a sub-field of artificial intelligence, it also has connections with theoretical computer science and philosophy.
In computer science, a term index is a data structure to facilitate fast lookup of terms and clauses in a logic program, deductive database, or automated theorem prover.
Ross A. Overbeek is an American computer scientist with a long tenure at the Argonne National Laboratory. He has made important contributions to mathematical logic and genomics, as well as programming, particularly in database theory and the programming language Prolog.
Prover9 is an automated theorem prover for first-order and equational logic developed by William McCune.
William Walker McCune was an American computer scientist and logician working in the fields of automated reasoning, algebra, logic, and formal methods.
The CADE ATP System Competition (CASC) is an annual competition of fully automated theorem provers for classical logic
Lawrence T. Wos (1930–2020) was an American mathematician, a researcher in the Mathematics and Computer Science Division of Argonne National Laboratory.
In mathematical logic, minimal axioms for Boolean algebra are assumptions which are equivalent to the axioms of Boolean algebra, chosen to be as short as possible. For example, an axiom with six NAND operations and three variables is equivalent to Boolean algebra:
In information technology a reasoning system is a software system that generates conclusions from available knowledge using logical techniques such as deduction and induction. Reasoning systems play an important role in the implementation of artificial intelligence and knowledge-based systems.
Models And Counter-Examples (Mace) is a model finder. Most automated theorem provers try to perform a proof by refutation on the clause normal form of the proof problem, by showing that the combination of axioms and negated conjecture can never be simultaneously true, i.e. does not have a model. A model finder such as Mace, on the other hand, tries to find an explicit model of a set of clauses. If it succeeds, this corresponds to a counter-example for the conjecture, i.e. it disproves the (claimed) theorem.



