
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances, named after French engineer and physicist Claude-Louis Navier and Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842-1850 (Stokes).
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:

Large eddy simulation (LES) is a mathematical model for turbulence used in computational fluid dynamics. It was initially proposed in 1963 by Joseph Smagorinsky to simulate atmospheric air currents, and first explored by Deardorff (1970). LES is currently applied in a wide variety of engineering applications, including combustion, acoustics, and simulations of the atmospheric boundary layer.

Smoothed-particle hydrodynamics (SPH) is a computational method used for simulating the mechanics of continuum media, such as solid mechanics and fluid flows. It was developed by Gingold and Monaghan and Lucy in 1977, initially for astrophysical problems. It has been used in many fields of research, including astrophysics, ballistics, volcanology, and oceanography. It is a meshfree Lagrangian method, and the resolution of the method can easily be adjusted with respect to variables such as density.
In fluid dynamics, the Reynolds stress is the component of the total stress tensor in a fluid obtained from the averaging operation over the Navier–Stokes equations to account for turbulent fluctuations in fluid momentum.
Fluid mechanics is the branch of physics concerned with the mechanics of fluids and the forces on them. It has applications in a wide range of disciplines, including mechanical, aerospace, civil, chemical and biomedical engineering, geophysics, oceanography, meteorology, astrophysics, and biology.

The lattice Boltzmann methods (LBM), originated from the lattice gas automata (LGA) method (Hardy-Pomeau-Pazzis and Frisch-Hasslacher-Pomeau models), is a class of computational fluid dynamics (CFD) methods for fluid simulation. Instead of solving the Navier–Stokes equations directly, a fluid density on a lattice is simulated with streaming and collision (relaxation) processes. The method is versatile as the model fluid can straightforwardly be made to mimic common fluid behaviour like vapour/liquid coexistence, and so fluid systems such as liquid droplets can be simulated. Also, fluids in complex environments such as porous media can be straightforwardly simulated, whereas with complex boundaries other CFD methods can be hard to work with.
In fluid dynamics, turbulence kinetic energy (TKE) is the mean kinetic energy per unit mass associated with eddies in turbulent flow. Physically, the turbulence kinetic energy is characterised by measured root-mean-square (RMS) velocity fluctuations. In the Reynolds-averaged Navier Stokes equations, the turbulence kinetic energy can be calculated based on the closure method, i.e. a turbulence model.

Sediment transport is the movement of solid particles (sediment), typically due to a combination of gravity acting on the sediment, and the movement of the fluid in which the sediment is entrained. Sediment transport occurs in natural systems where the particles are clastic rocks, mud, or clay; the fluid is air, water, or ice; and the force of gravity acts to move the particles along the sloping surface on which they are resting. Sediment transport due to fluid motion occurs in rivers, oceans, lakes, seas, and other bodies of water due to currents and tides. Transport is also caused by glaciers as they flow, and on terrestrial surfaces under the influence of wind. Sediment transport due only to gravity can occur on sloping surfaces in general, including hillslopes, scarps, cliffs, and the continental shelf—continental slope boundary.

The shallow-water equations (SWE) are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid. The shallow-water equations in unidirectional form are also called Saint-Venant equations, after Adhémar Jean Claude Barré de Saint-Venant.
The intent of this article is to highlight the important points of the derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
In a body submerged in a fluid, unsteady forces due to acceleration of that body with respect to the fluid, can be divided into two parts: the virtual mass effect and the Basset force.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
Ocean dynamics define and describe the motion of water within the oceans. Ocean temperature and motion fields can be separated into three distinct layers: mixed (surface) layer, upper ocean, and deep ocean.
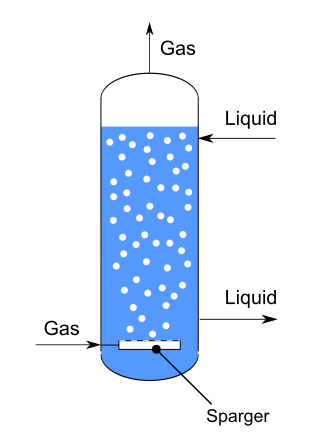
A bubble column reactor is a chemical reactor that belongs to the general class of multiphase reactors, which consists of three main categories: trickle bed reactor, fluidized bed reactor, and bubble column reactor. A bubble column reactor is a very simple device consisting of a vertical vessel filled with water with a gas distributor at the inlet. Due to the ease of design and operation, which does not involve moving parts, they are widely used in the chemical, biochemical, petrochemical, and pharmaceutical industries to generate and control gas-liquid chemical reactions.

In fluid dynamics, the radiation stress is the depth-integrated – and thereafter phase-averaged – excess momentum flux caused by the presence of the surface gravity waves, which is exerted on the mean flow. The radiation stresses behave as a second-order tensor.
The multiphase particle-in-cell method (MP-PIC) is a numerical method for modeling particle-fluid and particle-particle interactions in a computational fluid dynamics (CFD) calculation. The MP-PIC method achieves greater stability than its particle-in-cell predecessor by simultaneously treating the solid particles as computational particles and as a continuum. In the MP-PIC approach, the particle properties are mapped from the Lagrangian coordinates to an Eulerian grid through the use of interpolation functions. After evaluation of the continuum derivative terms, the particle properties are mapped back to the individual particles. This method has proven to be stable in dense particle flows, computationally efficient, and physically accurate. This has allowed the MP-PIC method to be used as particle-flow solver for the simulation of industrial-scale chemical processes involving particle-fluid flows.
In fluid dynamics, the Basset–Boussinesq–Oseen equation describes the motion of – and forces on – a small particle in unsteady flow at low Reynolds numbers. The equation is named after Joseph Valentin Boussinesq, Alfred Barnard Basset and Carl Wilhelm Oseen.
Computational Fluid Dynamics (CFD) modeling and simulation for phase change materials (PCMs) is a technique to analyze the performance and behavior of PCMs. The CFD models have been successful in studying and analyzing the air quality, natural ventilation and stratified ventilation, air flow initiated by buoyancy forces and temperature space for the systems integrated with PCMs. Simple shapes like flat plates, cylinders or annular tubes, fins, macro- and micro-encapsulations with containers of different shape are often modeled in CFD software's to study.




















