Related Research Articles

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation.
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space, which is one of the best models for the kissing number problem. It was discovered by John Leech (1967). It may also have been discovered by Ernst Witt in 1940.
23 (twenty-three) is the natural number following 22 and preceding 24.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another.
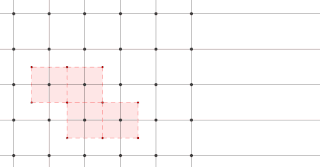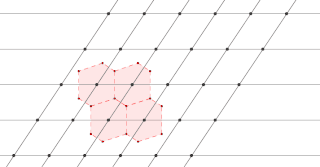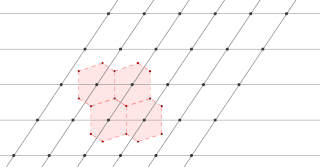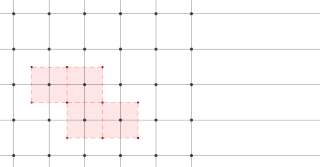
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a primitive cell which has been constructed by applying Voronoi decomposition to a crystal lattice. It is used in the study of crystalline materials in crystallography.
In geometry and mathematical group theory, a unimodular lattice is an integral lattice of determinant 1 or −1. For a lattice in n-dimensional Euclidean space, this is equivalent to requiring that the volume of any fundamental domain for the lattice be 1.
In mathematics, a Niemeier lattice is one of the 24 positive definite even unimodular lattices of rank 24, which were classified by Hans-Volker Niemeier (1973). Venkov (1978) gave a simplified proof of the classification. In the 1970s, Witt (1941) has a sentence mentioning that he found more than 10 such lattices in the 1940s, but gives no further details. One example of a Niemeier lattice is the Leech lattice found in 1967.
Miklós Ajtai is a computer scientist at the IBM Almaden Research Center, United States. In 2003, he received the Knuth Prize for his numerous contributions to the field, including a classic sorting network algorithm, exponential lower bounds, superlinear time-space tradeoffs for branching programs, and other "unique and spectacular" results. He is a member of the U.S. National Academy of Sciences.

In four-dimensional Euclidean geometry, the 16-cell honeycomb is one of the three regular space-filling tessellations, represented by Schläfli symbol {3,3,4,3}, and constructed by a 4-dimensional packing of 16-cell facets, three around every face.
The 5-demicube honeycomb is a uniform space-filling tessellation in Euclidean 5-space. It is constructed as an alternation of the regular 5-cube honeycomb.
The 7-demicubic honeycomb, or demihepteractic honeycomb is a uniform space-filling tessellation in Euclidean 7-space. It is constructed as an alternation of the regular 7-cubic honeycomb.
The 8-demicubic honeycomb, or demiocteractic honeycomb is a uniform space-filling tessellation in Euclidean 8-space. It is constructed as an alternation of the regular 8-cubic honeycomb.
In mathematics, the Coxeter–Todd lattice K12, discovered by Coxeter and Todd (1953), is a 12-dimensional even integral lattice of discriminant 36 with no norm-2 vectors. It is the sublattice of the Leech lattice fixed by a certain automorphism of order 3, and is analogous to the Barnes–Wall lattice. The automorphism group of the Coxeter–Todd lattice has order 210·37·5·7=78382080, and there are 756 vectors in this lattice of norm 4 (the shortest nonzero vectors in this lattice).
In mathematics, the Barnes–Wall lattice Λ16, discovered by Eric Stephen Barnes and G. E. (Tim) Wall (Barnes & Wall (1959)), is the 16-dimensional positive-definite even integral lattice of discriminant 28 with no norm-2 vectors. It is the sublattice of the Leech lattice fixed by a certain automorphism of order 2, and is analogous to the Coxeter–Todd lattice.
In mathematics, a eutactic lattice (or eutactic form) is a lattice in Euclidean space whose minimal vectors form a eutactic star. This means they have a set of positive eutactic coefficientsci such that (v, v) = Σci(v, mi)2 where the sum is over the minimal vectors mi. "Eutactic" is derived from the Greek language, and means "well-situated" or "well-arranged".
In mathematics, II25,1 is the even 26-dimensional Lorentzian unimodular lattice. It has several unusual properties, arising from Conway's discovery that it has a norm zero Weyl vector. In particular it is closely related to the Leech lattice Λ, and has the Conway group Co1 at the top of its automorphism group.
In digital signal processing, multidimensional sampling is the process of converting a function of a multidimensional variable into a discrete collection of values of the function measured on a discrete set of points. This article presents the basic result due to Petersen and Middleton on conditions for perfectly reconstructing a wavenumber-limited function from its measurements on a discrete lattice of points. This result, also known as the Petersen–Middleton theorem, is a generalization of the Nyquist–Shannon sampling theorem for sampling one-dimensional band-limited functions to higher-dimensional Euclidean spaces.
In the mathematical fields of numerical analysis and approximation theory, box splines are piecewise polynomial functions of several variables. Box splines are considered as a multivariate generalization of basis splines (B-splines) and are generally used for multivariate approximation/interpolation. Geometrically, a box spline is the shadow (X-ray) of a hypercube projected down to a lower-dimensional space. Box splines and simplex splines are well studied special cases of polyhedral splines which are defined as shadows of general polytopes.

In the area of modern algebra known as group theory, the Conway groupCo2 is a sporadic simple group of order
References
- Conway, John Horton; Sloane, N. J. A. (1988), "Low-dimensional lattices. III. Perfect forms", Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences, 418 (1854): 43–80, Bibcode:1988RSPSA.418...43C, doi:10.1098/rspa.1988.0073, ISSN 0962-8444, JSTOR 2398316, MR 0953277
- Conway, J. H.; Sloane, N. J. A. (1989). "Errata: Low-Dimensional Lattices. III. Perfect Forms". Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences. 426 (1871): 441. Bibcode:1989RSPSA.426..441C. doi:10.1098/rspa.1989.0134. JSTOR 2398351.
- Korkine; Zolotareff (1877), "Sur les formes quadratique positives", Mathematische Annalen , 11 (2): 242–292, doi:10.1007/BF01442667, ISSN 0025-5831
- Martinet, Jacques (2003), Perfect lattices in Euclidean spaces, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 327, Berlin, New York: Springer-Verlag, doi:10.1007/978-3-662-05167-2, ISBN 978-3-540-44236-3, MR 1957723
- Riener, Cordian (2006), "On extreme forms in dimension 8", Journal de théorie des nombres de Bordeaux, 18 (3): 677–682, doi: 10.5802/jtnb.565
- Sikirić, Mathieu Dutour; Schürmann, Achill; Vallentin, Frank (2007), "Classification of eight-dimensional perfect forms", Electronic Research Announcements of the American Mathematical Society, 13 (3): 21–32, arXiv: math/0609388 , doi:10.1090/S1079-6762-07-00171-0, ISSN 1079-6762, MR 2300003
- Venkov, Boris (2001), "Réseaux et designs sphériques, Réseaux euclidiens, designs sphériques et formes modulaires", Monographie de l'Enseignement Mathématique, 37: 10–86
- Voronoi, G. (1908), "Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Premier Mémoire: Sur quelques propriétés des formes quadratiques positives parfaites", Journal für die reine und angewandte Mathematik (in French), 1908 (133): 97–178, doi:10.1515/crll.1908.133.97, ISSN 0075-4102