Hebbian theory is a neuroscientific theory claiming that an increase in synaptic efficacy arises from a presynaptic cell's repeated and persistent stimulation of a postsynaptic cell. It is an attempt to explain synaptic plasticity, the adaptation of brain neurons during the learning process. It was introduced by Donald Hebb in his 1949 book The Organization of Behavior. The theory is also called Hebb's rule, Hebb's postulate, and cell assembly theory. Hebb states it as follows:
Let us assume that the persistence or repetition of a reverberatory activity tends to induce lasting cellular changes that add to its stability. ... When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A's efficiency, as one of the cells firing B, is increased.
In mathematics, the discrete-time Fourier transform (DTFT) is a form of Fourier analysis that is applicable to a sequence of values.

Neural oscillations, or brainwaves, are rhythmic or repetitive patterns of neural activity in the central nervous system. Neural tissue can generate oscillatory activity in many ways, driven either by mechanisms within individual neurons or by interactions between neurons. In individual neurons, oscillations can appear either as oscillations in membrane potential or as rhythmic patterns of action potentials, which then produce oscillatory activation of post-synaptic neurons. At the level of neural ensembles, synchronized activity of large numbers of neurons can give rise to macroscopic oscillations, which can be observed in an electroencephalogram. Oscillatory activity in groups of neurons generally arises from feedback connections between the neurons that result in the synchronization of their firing patterns. The interaction between neurons can give rise to oscillations at a different frequency than the firing frequency of individual neurons. A well-known example of macroscopic neural oscillations is alpha activity.
Sensory neuroscience is a subfield of neuroscience which explores the anatomy and physiology of neurons that are part of sensory systems such as vision, hearing, and olfaction. Neurons in sensory regions of the brain respond to stimuli by firing one or more nerve impulses following stimulus presentation. How is information about the outside world encoded by the rate, timing, and pattern of action potentials? This so-called neural code is currently poorly understood and sensory neuroscience plays an important role in the attempt to decipher it. Looking at early sensory processing is advantageous since brain regions that are "higher up" contain neurons which encode more abstract representations. However, the hope is that there are unifying principles which govern how the brain encodes and processes information. Studying sensory systems is an important stepping stone in our understanding of brain function in general.
Neural coding is a neuroscience field concerned with characterising the hypothetical relationship between the stimulus and the individual or ensemble neuronal responses and the relationship among the electrical activity of the neurons in the ensemble. Based on the theory that sensory and other information is represented in the brain by networks of neurons, it is thought that neurons can encode both digital and analog information.
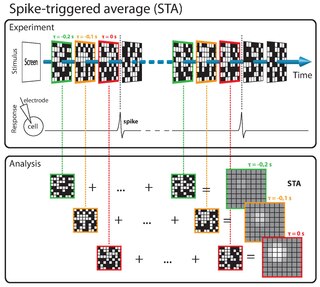
The spike-triggered average (STA) is a tool for characterizing the response properties of a neuron using the spikes emitted in response to a time-varying stimulus. The STA provides an estimate of a neuron's linear receptive field. It is a useful technique for the analysis of electrophysiological data.
In computational neuroscience, the Wilson–Cowan model describes the dynamics of interactions between populations of very simple excitatory and inhibitory model neurons. It was developed by Hugh R. Wilson and Jack D. Cowan and extensions of the model have been widely used in modeling neuronal populations. The model is important historically because it uses phase plane methods and numerical solutions to describe the responses of neuronal populations to stimuli. Because the model neurons are simple, only elementary limit cycle behavior, i.e. neural oscillations, and stimulus-dependent evoked responses are predicted. The key findings include the existence of multiple stable states, and hysteresis, in the population response.

Biological neuron models, also known as a spiking neuron models, are mathematical descriptions of the properties of certain cells in the nervous system that generate sharp electrical potentials across their cell membrane, roughly one millisecond in duration, called action potentials or spikes. Since spikes are transmitted along the axon and synapses from the sending neuron to many other neurons, spiking neurons are considered to be a major information processing unit of the nervous system. Spiking neuron models can be divided into different categories: the most detailed mathematical models are biophysical neuron models that describe the membrane voltage as a function of the input current and the activation of ion channels. Mathematically simpler are integrate-and-fire models that describe the membrane voltage as a function of the input current and predict the spike times without a description of the biophysical processes that shape the time course of an action potential. Even more abstract models only predict output spikes as a function of the stimulation where the stimulation can occur through sensory input or pharmacologically. This articles provides a short overview of different spiking neuron models and links, whenever possible to experimental phenomena. It includes deterministic and probabilistic models.
Two-alternative forced choice (2AFC) is a method for measuring the sensitivity of a person, child or infant, or animal to some particular sensory input, stimulus, through that observer's pattern of choices and response times to two versions of the sensory input. For example, to determine a person's sensitivity to dim light, the observer would be presented with a series of trials in which a dim light was randomly either in the top or bottom of the display. After each trial, the observer responds "top" or "bottom". The observer is not allowed to say "I do not know", or "I am not sure", or "I did not see anything". In that sense the observer's choice is forced between the two alternatives.

The linear-nonlinear-Poisson (LNP) cascade model is a simplified functional model of neural spike responses. It has been successfully used to describe the response characteristics of neurons in early sensory pathways, especially the visual system. The LNP model is generally implicit when using reverse correlation or the spike-triggered average to characterize neural responses with white-noise stimuli.
Spike-triggered covariance (STC) analysis is a tool for characterizing a neuron's response properties using the covariance of stimuli that elicit spikes from a neuron. STC is related to the spike-triggered average (STA), and provides a complementary tool for estimating linear filters in a linear-nonlinear-Poisson (LNP) cascade model. Unlike STA, the STC can be used to identify a multi-dimensional feature space in which a neuron computes its response.
Neural decoding is a neuroscience field concerned with the hypothetical reconstruction of sensory and other stimuli from information that has already been encoded and represented in the brain by networks of neurons. Reconstruction refers to the ability of the researcher to predict what sensory stimuli the subject is receiving based purely on neuron action potentials. Therefore, the main goal of neural decoding is to characterize how the electrical activity of neurons elicit activity and responses in the brain.

The theta model, or Ermentrout–Kopell canonical model, is a biological neuron model originally developed to model neurons in the animal Aplysia, and later used in various fields of computational neuroscience. The model is particularly well suited to describe neuron bursting, which are rapid oscillations in the membrane potential of a neuron interrupted by periods of relatively little oscillation. Bursts are often found in neurons responsible for controlling and maintaining steady rhythms. For example, breathing is controlled by a small network of bursting neurons in the brain stem. Of the three main classes of bursting neurons, the theta model describes parabolic bursting. Parabolic bursting is characterized by a series of bursts that are regulated by a slower external oscillation. This slow oscillation changes the frequency of the faster oscillation so that the frequency curve of the burst pattern resembles a parabola.
Exponential integrate-and-fire models are compact and computationally efficient nonlinear spiking neuron models with one or two variables. The exponential integrate-and-fire model was first proposed as a one-dimensional model. The most prominent two-dimensional examples are the adaptive exponential integrate-and-fire model and the generalized exponential integrate-and-fire model. Exponential integrate-and-fire models are widely used in the field of computational neuroscience and spiking neural networks because of (i) a solid grounding of the neuron model in the field of experimental neuroscience, (ii) computational efficiency in simulations and hardware implementations, and (iii) mathematical transparency.
Maximally informative dimensions is a dimensionality reduction technique used in the statistical analyses of neural responses. Specifically, it is a way of projecting a stimulus onto a low-dimensional subspace so that as much information as possible about the stimulus is preserved in the neural response. It is motivated by the fact that natural stimuli are typically confined by their statistics to a lower-dimensional space than that spanned by white noise but correctly identifying this subspace using traditional techniques is complicated by the correlations that exist within natural images. Within this subspace, stimulus-response functions may be either linear or nonlinear. The idea was originally developed by Tatyana Sharpee, Nicole Rust, and William Bialek in 2003.
Biological motion perception is the act of perceiving the fluid unique motion of a biological agent. The phenomenon was first documented by Swedish perceptual psychologist, Gunnar Johansson, in 1973. There are many brain areas involved in this process, some similar to those used to perceive faces. While humans complete this process with ease, from a computational neuroscience perspective there is still much to be learned as to how this complex perceptual problem is solved. One tool which many research studies in this area use is a display stimuli called a point light walker. Point light walkers are coordinated moving dots that simulate biological motion in which each dot represents specific joints of a human performing an action.
In computational neuroscience, SUPS or formerly CUPS is a measure of a neuronal network performance, useful in fields of neuroscience, cognitive science, artificial intelligence, and computer science.
A binding neuron (BN) is an abstract concept of processing of input impulses in a generic neuron based on their temporal coherence and the level of neuronal inhibition. Mathematically, the concept may be implemented by most neuronal models including the well-known leaky integrate-and-fire model. The BN concept originated in 1996 and 1998 papers by A. K. Vidybida,
The Tempotron is a supervised synaptic learning algorithm which is applied when the information is encoded in spatiotemporal spiking patterns. This is an advancement of the perceptron which does not incorporate a spike timing framework.
The Spike Response Model (SRM) is a spiking neuron model in which spikes are generated by either a deterministic or a stochastic threshold process. In the SRM, the membrane voltage V is described as a linear sum of the postsynaptic potentials (PSPs) caused by spike arrivals to which the effects of refractoriness and adaptation are added. The threshold is either fixed or dynamic. In the latter case it increases after each spike. The SRM is flexible enough to account for a variety of neuronal firing pattern in response to step current input. The SRM has also been used in the theory of computation to quantify the capacity of spiking neural networks; and in the neurosciences to predict the subthreshold voltage and the firing times of cortical neurons during stimulation with a time-dependent current stimulation. The name Spike Response Model points to the property that the two important filters and of the model can be interpreted as the response of the membrane potential to an incoming spike and to an outgoing spike. The SRM has been formulated in continuous time and in discrete time. The SRM can be viewed as a Generalized Linear Model (GLM) or as an a generalized integrate-and-fire model with adaptation.







