Other
The concept of piecewise-defined functions is often generalized:
- Piecewise linear curve
- Piecewise polynomial curve, also known as a spline (mathematics)
- Piecewise linear manifold
In mathematics, piecewise properties may be exemplified in:
A function property holds piecewise for a function, if the function can be piecewise-defined in a way that the property holds for every subdomain. Examples of functions with such piecewise properties are:
The concept of piecewise-defined functions is often generalized:
In mathematics, an equation is a mathematical formula that expresses the equality of two expressions, by connecting them with the equals sign =. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English, any well-formed formula consisting of two expressions related with an equals sign is an equation.

In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation. Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or determining displacement from velocity. Usage of integration expanded to a wide variety of scientific fields thereafter.

In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.

In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having only finitely many pieces.

Non-uniform rational basis spline (NURBS) is a mathematical model using basis splines (B-splines) that is commonly used in computer graphics for representing curves and surfaces. It offers great flexibility and precision for handling both analytic and modeled shapes. It is a type of curve modeling, as opposed to polygonal modeling or digital sculpting. NURBS curves are commonly used in computer-aided design (CAD), manufacturing (CAM), and engineering (CAE). They are part of numerous industry-wide standards, such as IGES, STEP, ACIS, and PHIGS. Tools for creating and editing NURBS surfaces are found in various 3D graphics, rendering, and animation software packages.
In mathematical analysis, a space-filling curve is a curve whose range reaches every point in a higher dimensional region, typically the unit square. Because Giuseppe Peano (1858–1932) was the first to discover one, space-filling curves in the 2-dimensional plane are sometimes called Peano curves, but that phrase also refers to the Peano curve, the specific example of a space-filling curve found by Peano.
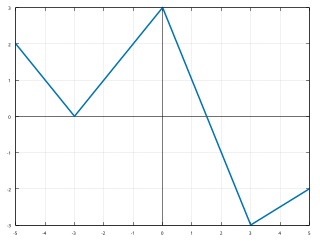
In mathematics, a piecewise function is a function whose domain is partitioned into several intervals ("subdomains") on which the function may be defined differently. Piecewise definition is actually a way of specifying the function, rather than a characteristic of the resulting function itself.

In complex analysis, a branch of mathematics, Morera's theorem, named after Giacinto Morera, gives an important criterion for proving that a function is holomorphic.
In mathematics, a piecewise linear or segmented function is a real-valued function of a real variable, whose graph is composed of straight-line segments.
In mathematics, a piecewise linear manifold is a topological manifold together with a piecewise linear structure on it. Such a structure can be defined by means of an atlas, such that one can pass from chart to chart in it by piecewise linear functions. This is slightly stronger than the topological notion of a triangulation. An isomorphism of PL manifolds is called a PL homeomorphism.
Piecewise linear may refer to:
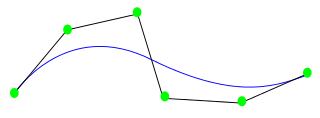
In geometric topology, PDIFF, for piecewise differentiable, is the category of piecewise-smooth manifolds and piecewise-smooth maps between them. It properly contains DIFF and PL, and the reason it is defined is to allow one to relate these two categories. Further, piecewise functions such as splines and polygonal chains are common in mathematics, and PDIFF provides a category for discussing them.

In geometry, a polygonal chain is a connected series of line segments. More formally, a polygonal chain is a curve specified by a sequence of points called its vertices. The curve itself consists of the line segments connecting the consecutive vertices.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted or . It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.

The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat transfer, fluid flow, mass transport, and electromagnetic potential.

In mathematics, more specifically in differential geometry and topology, various types of functions between manifolds are studied, both as objects in their own right and for the light they shed
In mathematics, the Schoenflies problem or Schoenflies theorem, of geometric topology is a sharpening of the Jordan curve theorem by Arthur Schoenflies. For Jordan curves in the plane it is often referred to as the Jordan–Schoenflies theorem.

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. There are many other equivalent definitions of these curves, going back to Archimedes. Examples of convex curves include the convex polygons, the boundaries of convex sets, and the graphs of convex functions. Important subclasses of convex curves include the closed convex curves, the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve.
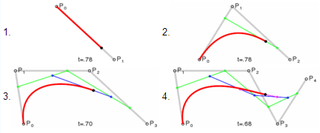
In mathematics, the variation diminishing property of certain mathematical objects involves diminishing the number of changes in sign.

In numerical mathematics, the gradient discretisation method (GDM) is a framework which contains classical and recent numerical schemes for diffusion problems of various kinds: linear or non-linear, steady-state or time-dependent. The schemes may be conforming or non-conforming, and may rely on very general polygonal or polyhedral meshes.