
Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometrical problems. Classically, it studies zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects.
In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the x or y coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

In mathematics, the Roman surface or Steiner surface is a self-intersecting mapping of the real projective plane into three-dimensional space, with an unusually high degree of symmetry. This mapping is not an immersion of the projective plane; however, the figure resulting from removing six singular points is one. Its name arises because it was discovered by Jakob Steiner when he was in Rome in 1844.

In geometry, a paraboloid is a quadric surface that has exactly one axis of symmetry and no center of symmetry. The term "paraboloid" is derived from parabola, which refers to a conic section that has a similar property of symmetry.
In mathematics, complex geometry is the study of geometric structures and constructions arising out of, or described by, the complex numbers. In particular, complex geometry is concerned with the study of spaces such as complex manifolds and complex algebraic varieties, functions of several complex variables, and holomorphic constructions such as holomorphic vector bundles and coherent sheaves. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric aspects of complex analysis.

In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane curve can be completed in a projective algebraic plane curve by homogenizing its defining polynomial. Conversely, a projective algebraic plane curve of homogeneous equation h(x, y, t) = 0 can be restricted to the affine algebraic plane curve of equation h(x, y, 1) = 0. These two operations are each inverse to the other; therefore, the phrase algebraic plane curve is often used without specifying explicitly whether it is the affine or the projective case that is considered.

In mathematics, a cubic surface is a surface in 3-dimensional space defined by one polynomial equation of degree 3. Cubic surfaces are fundamental examples in algebraic geometry. The theory is simplified by working in projective space rather than affine space, and so cubic surfaces are generally considered in projective 3-space . The theory also becomes more uniform by focusing on surfaces over the complex numbers rather than the real numbers; note that a complex surface has real dimension 4. A simple example is the Fermat cubic surface

In geometry, a locus is a set of all points, whose location satisfies or is determined by one or more specified conditions.
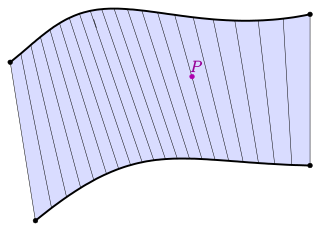
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. Examples include the plane, the lateral surface of a cylinder or cone, a conical surface with elliptical directrix, the right conoid, the helicoid, and the tangent developable of a smooth curve in space.

In geometry, Villarceau circles are a pair of circles produced by cutting a torus obliquely through its center at a special angle.

In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.

In geometry, the Whitney umbrella is a specific self-intersecting ruled surface placed in three dimensions. It is the union of all straight lines that pass through points of a fixed parabola and are perpendicular to a fixed straight line which is parallel to the axis of the parabola and lies on its perpendicular bisecting plane.
In mathematics, in the theory of ordinary differential equations in the complex plane , the points of are classified into ordinary points, at which the equation's coefficients are analytic functions, and singular points, at which some coefficient has a singularity. Then amongst singular points, an important distinction is made between a regular singular point, where the growth of solutions is bounded by an algebraic function, and an irregular singular point, where the full solution set requires functions with higher growth rates. This distinction occurs, for example, between the hypergeometric equation, with three regular singular points, and the Bessel equation which is in a sense a limiting case, but where the analytic properties are substantially different.

In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.
In algebraic geometry, a quartic plane curve is a plane algebraic curve of the fourth degree. It can be defined by a bivariate quartic equation:

In algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation
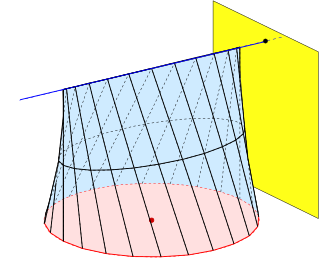
In geometry a conoid is a ruled surface, whose rulings (lines) fulfill the additional conditions:
In mathematics, a translation of axes in two dimensions is a mapping from an xy-Cartesian coordinate system to an x'y'-Cartesian coordinate system in which the x' axis is parallel to the x axis and k units away, and the y' axis is parallel to the y axis and h units away. This means that the origin O' of the new coordinate system has coordinates (h, k) in the original system. The positive x' and y' directions are taken to be the same as the positive x and y directions. A point P has coordinates (x, y) with respect to the original system and coordinates (x', y') with respect to the new system, where
In Euclidean geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse, which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle; the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle; and the Artzt parabolas, which are parabolas touching two sidelines of the reference triangle at vertices of the triangle.























